题目内容
5.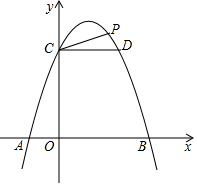 二次函数y=-x2+2x+3的图象与x轴交于A,B两点(点A在B的左侧),与y轴交于点C,过点C作y轴的垂线交抛物线于另一点D.
二次函数y=-x2+2x+3的图象与x轴交于A,B两点(点A在B的左侧),与y轴交于点C,过点C作y轴的垂线交抛物线于另一点D.(1)①求OA,OB,OC的长;
②直接写出点D的坐标(2,3);
(2)已知点P位于第一象限且在抛物线上,它的横坐标为$\frac{5}{3}$,求证:∠ACB=∠PCB.
分析 (1)①令0=-x2+2x+3,解方程即可得到结论;②根据抛物线y=-x2+2x+3求得对称轴为x=-$\frac{2}{2×(-1)}$=1,根据轴对称的性质即可得到结论;
(2)连接AC,BC,过P作PE⊥CD于E,解直角三角形即可得到结论.
解答 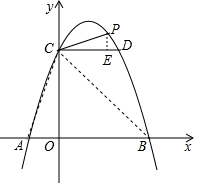 解:(1)①令0=-x2+2x+3,解得:x1=-1,x2=3,令x=0,则y=3,
解:(1)①令0=-x2+2x+3,解得:x1=-1,x2=3,令x=0,则y=3,
∴OA=1,OB=3,OC=3;
②抛物线y=-x2+2x+3的对称轴为x=-$\frac{2}{2×(-1)}$=1,C(0,3),
由题意知,C,D关于直线x=1为对称,设D(m,3),
∴$\frac{m+0}{2}$=1,
∴m=2,
∴D(2,3),
故答案为:(2,3);
(2)连接AC,BC,过P作PE⊥CD于E,
当x=$\frac{5}{3}$时,y=-($\frac{5}{3}$)2+2×$\frac{5}{3}$+3=$\frac{32}{9}$,
∴PE=$\frac{32}{9}$-3=$\frac{5}{9}$,CE=$\frac{5}{3}$,
∴tan∠PCD=$\frac{PE}{CE}$=$\frac{\frac{5}{9}}{\frac{5}{3}}$=$\frac{1}{3}$,tan∠ACO=$\frac{OA}{OC}$=$\frac{1}{3}$,
∴∠PCD=∠ACO,
∵CD⊥OC,OC⊥OB,OB=OC=3,
∴∠BCO=45°,∠DCB=90°-45°=45°,
∴∠BCO=∠DCB,
∴∠ACB=∠PCB.
点评 本题考查了二次函数图象上点的坐标特征,解直角三角形,轴对称的性质,等腰直角三角形的判定和性质,正确的作出辅助线是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
16.在下列命题中:
①同旁内角互补;
②两点确定一条直线;
③两条直线相交,有且只有一个交点;
④若一个角的两边分别与另一个角的两边平行,那么这两个角相等.
其中属于真命题的有( )
①同旁内角互补;
②两点确定一条直线;
③两条直线相交,有且只有一个交点;
④若一个角的两边分别与另一个角的两边平行,那么这两个角相等.
其中属于真命题的有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
20.下列运算正确的是( )
| A. | a6÷a2=a4 | B. | (a2)3=a5 | C. | a2•a3=a6 | D. | a2+2a2=3a4 |
10.如图1,菱形纸片ABCD的边长为2,∠ABC=60°,将菱形ABCD沿EF,GH折叠,使得点B,D两点重合于对角线BD上一点P(如图2),则六边形AEFCHG面积的最大值是( )
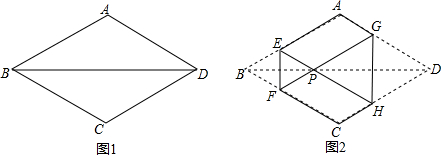

| A. | $\frac{3\sqrt{3}}{2}$ | B. | $\frac{3\sqrt{3}}{4}$ | C. | 2-$\sqrt{3}$ | D. | 1+$\sqrt{3}$ |
14.下列命题中是真命题的是( )
| A. | 如果m是实数,那么m是有理数 | B. | -5没有立方根 | ||
| C. | 互补的角一定的邻补角 | D. | 正数不全是有理数 |
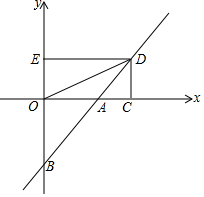 如图,直线y=x+b(b≠0)交坐标轴于A、B两点,点D(2,n)在直线AB上,过D作两坐标的垂线DC、DE,垂足分别为C,E,连接OD.若四边形OCDE的面积为2,
如图,直线y=x+b(b≠0)交坐标轴于A、B两点,点D(2,n)在直线AB上,过D作两坐标的垂线DC、DE,垂足分别为C,E,连接OD.若四边形OCDE的面积为2, 如图,在平面直角坐标系中,二次函数的图象交坐标轴于A(-1,0),B(4,0),C(0,-4)三点,点P是直线BC下方抛物线上一动点.
如图,在平面直角坐标系中,二次函数的图象交坐标轴于A(-1,0),B(4,0),C(0,-4)三点,点P是直线BC下方抛物线上一动点. 如图,点E、C在线段BF上,BE=CF,AB=DE,AC=DF.求证:∠ABC=∠DEF.
如图,点E、C在线段BF上,BE=CF,AB=DE,AC=DF.求证:∠ABC=∠DEF.