题目内容
15. 如图,点E、C在线段BF上,BE=CF,AB=DE,AC=DF.求证:∠ABC=∠DEF.
如图,点E、C在线段BF上,BE=CF,AB=DE,AC=DF.求证:∠ABC=∠DEF.
分析 先证明△ABC≌△DEF,然后利用全等三角形的性质即可求出∠ABC=∠DEF.
解答 解:∵BE=CF,
∴BE+EC=CF+EC,
∴BC=EF,
在△ABC与△DEF中,
$\left\{\begin{array}{l}{AB=DE}\\{BC=EF}\\{AC=DF}\end{array}\right.$
∴△ABC≌△DEF(SSS)
∴∠ABC=∠DEF
点评 本题考查全等三角形的判定与性质,解题的关键是熟练运用全等三角形的判定,本题属于基础题型.

练习册系列答案
相关题目
6.在下面四个几何体中,俯视图是三角形的是( )
| A. |  | B. |  | C. |  | D. |  |
3.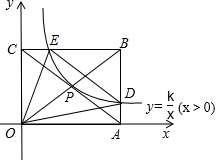 如图,矩形OABC的顶点A、C坐标分别是(8,0),(0,4),反比例函数y=$\frac{k}{x}$(x>0)的图象过对角线的交点P并且与AB、BC分别交于D、E两点,连接OD、OE、DE,则△ODE的面积为( )
如图,矩形OABC的顶点A、C坐标分别是(8,0),(0,4),反比例函数y=$\frac{k}{x}$(x>0)的图象过对角线的交点P并且与AB、BC分别交于D、E两点,连接OD、OE、DE,则△ODE的面积为( )
 如图,矩形OABC的顶点A、C坐标分别是(8,0),(0,4),反比例函数y=$\frac{k}{x}$(x>0)的图象过对角线的交点P并且与AB、BC分别交于D、E两点,连接OD、OE、DE,则△ODE的面积为( )
如图,矩形OABC的顶点A、C坐标分别是(8,0),(0,4),反比例函数y=$\frac{k}{x}$(x>0)的图象过对角线的交点P并且与AB、BC分别交于D、E两点,连接OD、OE、DE,则△ODE的面积为( )| A. | 14 | B. | 12 | C. | 15 | D. | 8 |
10.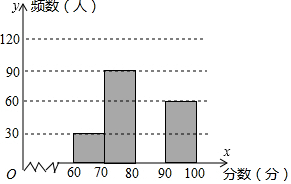 为了了解我市中学生参加“科普知识”竞赛成绩的情况,随机抽查了部分参赛学生的成绩,整理并制作出如下的统计表和统计图,如图所示.请根据图表信息解答下列问题:
为了了解我市中学生参加“科普知识”竞赛成绩的情况,随机抽查了部分参赛学生的成绩,整理并制作出如下的统计表和统计图,如图所示.请根据图表信息解答下列问题:
(1)在表中:m=120,n=0.3;
(2)补全频数分布直方图;
(3)小明的成绩是所有被抽查学生成绩的中位数,据此推断他的成绩在C组;
(4)4个小组每组推荐1人,然后从4人中随机抽取2人参加颁奖典礼,恰好抽中A、C两组学生的概率是多少?并列表或画树状图说明.
 为了了解我市中学生参加“科普知识”竞赛成绩的情况,随机抽查了部分参赛学生的成绩,整理并制作出如下的统计表和统计图,如图所示.请根据图表信息解答下列问题:
为了了解我市中学生参加“科普知识”竞赛成绩的情况,随机抽查了部分参赛学生的成绩,整理并制作出如下的统计表和统计图,如图所示.请根据图表信息解答下列问题:| 组别 | 分数段(分) | 频数 | 频率 |
| A组 | 60≤x<70 | 30 | 0.1 |
| B组 | 70≤x<80 | 90 | n |
| C组 | 80≤x<90 | m | 0.4 |
| D组 | 90≤x<100 | 60 | 0.2 |
(2)补全频数分布直方图;
(3)小明的成绩是所有被抽查学生成绩的中位数,据此推断他的成绩在C组;
(4)4个小组每组推荐1人,然后从4人中随机抽取2人参加颁奖典礼,恰好抽中A、C两组学生的概率是多少?并列表或画树状图说明.
7.下列说法中错误的是( )
| A. | 三角形的一个外角大于任何一个内角 | |
| B. | 任意多边形的外角和都是360° | |
| C. | 三角形任一边上的中线把原三角形分成两个面积相等的三角形 | |
| D. | 三角形的中线、角平分线、高线都是线段 |
4.若数据10,9,a,12,9的平均数是10,则这组数据的方差是( )
| A. | 1 | B. | 1.2 | C. | 0.9 | D. | 1.4 |
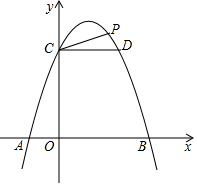 二次函数y=-x2+2x+3的图象与x轴交于A,B两点(点A在B的左侧),与y轴交于点C,过点C作y轴的垂线交抛物线于另一点D.
二次函数y=-x2+2x+3的图象与x轴交于A,B两点(点A在B的左侧),与y轴交于点C,过点C作y轴的垂线交抛物线于另一点D.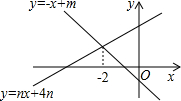 如图,直线y=-x+m与y=nx+4n(n≠0)的交点的横坐标为-2,则关于x的不等式-x+m>nx+4n>0的整数解为( )
如图,直线y=-x+m与y=nx+4n(n≠0)的交点的横坐标为-2,则关于x的不等式-x+m>nx+4n>0的整数解为( )