题目内容
如图，已知四边形ABED∽四边形BCGF∽四边形CAIH，记四边形ABED、四边形BFGC和四边形CAIH的面积分别为S3、S2、S1，若S1+S2=S3，求证：△ABC为直角三角形．考点：面积及等积变换
专题：证明题
分析：要证明△ABC是直角三角形，可以转化成证明AC2+BC2=AB2．又S1、S2和S3的比可转化成△ABC的三边平方的比，再利用S1+S2=S3，便可得到AC2+BC2=AB2．
解答：
证明：∵四边形ABED∽四边形BCGF∽四边形CAIH，
∴
=
，
=
，
∴
+
=
+
，
即
=
，而S1+S2=S3，
∴AC2+BC2=AB2，
∴△ABC为直角三角形．
证明：∵四边形ABED∽四边形BCGF∽四边形CAIH，∴
| S1 |
| S3 |
| AC2 |
| AB2 |
| S2 |
| S3 |
| BC2 |
| AB2 |
∴
| S1 |
| S3 |
| S2 |
| S3 |
| AC2 |
| AB2 |
| BC2 |
| AB2 |
即
| S1+S2 |
| S3 |
| AC2+BC2 |
| AB2 |
∴AC2+BC2=AB2，
∴△ABC为直角三角形．
点评：此题主要考查了相似图形的性质以及勾股定理逆定理等知识，得出
=
是解题关键．
| S1+S2 |
| S3 |
| AC2+BC2 |
| AB2 |
练习册系列答案
相关题目
如图，两个圆的圆心相同，它们的面积分别是12.56和25.12，求圆环的宽度d（π取3.14，结果保留小数点后两位）．直线y=2x-6与两坐标轴所围成的三角形面积等于（ ）
| A、18 | B、6 | C、12 | D、9 |
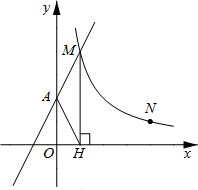如图，直线y1=2x+2与y轴交于A点，与反比例函数y2=
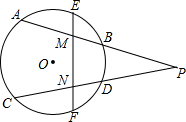如图，已知圆O的弦AB、CD的延长线相交于点P，连接弧AB、弧CD的中点E、F分别交AB、CD于点M、N，求证：△PNM是等腰三角形．