题目内容
6.已知x=$\sqrt{2}-1$,则$\frac{x}{{x}^{2}-1}÷(1+\frac{1}{x-1})$=$\frac{\sqrt{2}}{2}$.分析 将被除式分母因式分解,计算括号内分式的加法,再将除法转化为乘法,计算乘法可化简原式,将x的值代入计算可得.
解答 解:原式=$\frac{x}{(x+1)(x-1)}$÷$\frac{x}{x-1}$
=$\frac{x}{(x+1)(x-1)}$•$\frac{x-1}{x}$
=$\frac{1}{x+1}$,
当x=$\sqrt{2}$-1时,
原式=$\frac{1}{\sqrt{2}-1+1}$=$\frac{\sqrt{2}}{2}$.
故答案为:$\frac{\sqrt{2}}{2}$.
点评 本题主要考查分式的化简求值,熟练掌握分式的基本性质和分式运算的法则是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13.无理数-$\sqrt{2}$的相反数是( )
| A. | -$\sqrt{2}$ | B. | $\sqrt{2}$ | C. | $\frac{1}{\sqrt{2}}$ | D. | -$\frac{1}{\sqrt{2}}$ |
 x2+bx+c
x2+bx+c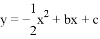 与y轴交于点C,与x轴的两个交点分别为A(﹣4,0),B(1,0).
与y轴交于点C,与x轴的两个交点分别为A(﹣4,0),B(1,0).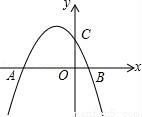
 得( )
得( )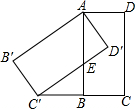 如图,将矩形ABCD绕点A顺时针旋转,得到矩形AB′C′D′,点C的对应点C′恰好落在CB的延长线上,边AB交边C′D′于点E.
如图,将矩形ABCD绕点A顺时针旋转,得到矩形AB′C′D′,点C的对应点C′恰好落在CB的延长线上,边AB交边C′D′于点E. B.
B. 

 D. 以上都不是
D. 以上都不是