题目内容
如图，已知△ABC，以AB、AC为边向外作正方形ABFD和正方形ACGE．连接BE，CD．BE与CD有什么数量关系？简单说明理由．考点：全等三角形的判定与性质,正方形的性质
专题：
分析：BE与CD数量关系是相等，由正方形的性质就可以得出△ADC≌△ABE，就可以得出CD=BE
解答：解：CD=BE．
理由如下：
∵四边形ABFD和四边形ACGE都是正方形，
∴AD=AB，AC=AE，∠DAB=∠CAE=90°，
∴∠DAB+∠BAC=∠CAE+∠BAC，
∴∠DAC=∠BAE．
在△ADC和△ABE中，
，
∴△ADC≌△ABE（SAS），
∴CD=BE．
理由如下：
∵四边形ABFD和四边形ACGE都是正方形，
∴AD=AB，AC=AE，∠DAB=∠CAE=90°，
∴∠DAB+∠BAC=∠CAE+∠BAC，
∴∠DAC=∠BAE．
在△ADC和△ABE中，
|
∴△ADC≌△ABE（SAS），
∴CD=BE．
点评：此题考查了正方形的性质，涉及的知识有：全等三角形的判定与性质，熟练掌握全等三角形的判定与性质是解本题的关键．
练习册系列答案
阅读快车系列答案
相关题目
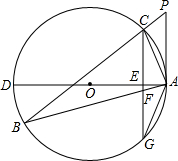如图，△ABC为⊙O的内接三角形，P为BC延长线上一点，∠PAC=∠B，AD为⊙O的直径，过C作CG⊥AD交AD于E，交AB于F，交⊙O于G．
