题目内容
数学课上,张老师正在上课:同学们,我们学过四个顶点在圆上的四边形是圆内接四边形,圆内接四边形的对角(相对的两个角)互补.下面我们来研究它外角的性质.
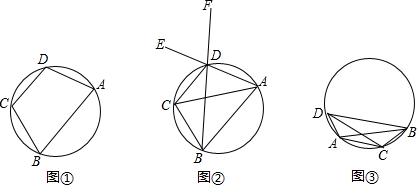
(1)在图①中作出圆内接四边形ABCD中以点C为顶点的外角∠DCE,并请你探究外角∠DCE与它的相邻内角的对角(简称内对角)∠A的关系,并证明∠DCE与∠A的关系;
(2)分别延长BD、AD到点F、E,如图②,已知四边形ABCD是圆内接四边形,如果DE平分∠FDC,请你探索AB与AC有怎样的数量关系呢?
(3)如图③,点D是圆上一点,弦AB=
,DC是∠ADB的平分线,∠BAC=30°.当∠DAC等于多少度时,四边形DACB有最大面积?最大面积是多少?

(1)在图①中作出圆内接四边形ABCD中以点C为顶点的外角∠DCE,并请你探究外角∠DCE与它的相邻内角的对角(简称内对角)∠A的关系,并证明∠DCE与∠A的关系;
(2)分别延长BD、AD到点F、E,如图②,已知四边形ABCD是圆内接四边形,如果DE平分∠FDC,请你探索AB与AC有怎样的数量关系呢?
(3)如图③,点D是圆上一点,弦AB=
| 3 |
考点:圆的综合题
专题:
分析:(1)根据圆内接四边形对角互补的性质即可得出结论;
(2)先根据四边形ABCD是圆内接四边形得出∠2=∠ABC,再根据∠1=∠ADB,∠ADB=∠ACB得出∠1=∠ACB,由DE平分∠FDC可知∠1=∠2所以∠ABC=∠ACB,由此可得出结论;
(3)根据DC平分∠ADB可知∠ADC=∠BDC,再由∠ADC=∠ABC,∠BDC=∠BAC,得出∠ABC=∠BAC,进而AC=BC,由直角三角形的性质得出AC=BC=1,由于S四边形DACB=S△ABC+S△DAB
S△ABC为定值,当S△DAB最大时,四边形DACB面积最大,要使四边形DACB面积最大,只需求出面积最大的△DAB 即可在△DAB中,AB边不变,当点D是AB的中垂线与圆的交点时,四边形DACB面积最大,此时△DAB为等边三角形,此时DC应为圆的直径,∠DAC=90°,根据∠ADC=∠BAC=30°可知DC=2AC=2,由此可得出结论.
(2)先根据四边形ABCD是圆内接四边形得出∠2=∠ABC,再根据∠1=∠ADB,∠ADB=∠ACB得出∠1=∠ACB,由DE平分∠FDC可知∠1=∠2所以∠ABC=∠ACB,由此可得出结论;
(3)根据DC平分∠ADB可知∠ADC=∠BDC,再由∠ADC=∠ABC,∠BDC=∠BAC,得出∠ABC=∠BAC,进而AC=BC,由直角三角形的性质得出AC=BC=1,由于S四边形DACB=S△ABC+S△DAB
S△ABC为定值,当S△DAB最大时,四边形DACB面积最大,要使四边形DACB面积最大,只需求出面积最大的△DAB 即可在△DAB中,AB边不变,当点D是AB的中垂线与圆的交点时,四边形DACB面积最大,此时△DAB为等边三角形,此时DC应为圆的直径,∠DAC=90°,根据∠ADC=∠BAC=30°可知DC=2AC=2,由此可得出结论.
解答: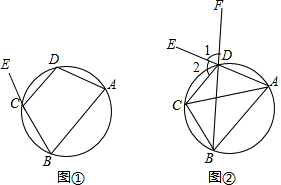 解:(1)画图如图,∠DCE=∠A.
解:(1)画图如图,∠DCE=∠A.
证明:∵四边形ABCD是圆内接四边形,
∴∠A+∠BCD=180°,
∴∠DCE+∠BCD=180°
∠DCE=∠A;
(2)AB=AC,
证明:∵四边形ABCD是圆内接四边形,
∴∠2=∠ABC,
∵∠1=∠ADB,∠ADB=∠ACB,
∴∠1=∠ACB,
∵DE平分∠FDC,
∴∠1=∠2,
∴∠ABC=∠ACB,
∴AB=AC;
(3)∵DC平分∠ADB,
∴∠ADC=∠BDC,
又∵∠ADC=∠ABC,∠BDC=∠BAC,
∴∠ABC=∠BAC,
∴AC=BC,
∵AB=
,∠BAC=30°,
∴AC=BC=1,
∵S四边形DACB=S△ABC+S△DAB
S△ABC为定值,当S△DAB最大时,四边形DACB面积最大,
要使四边形DACB面积最大,只需求出面积最大的△DAB 即可
在△DAB中,AB边不变,当点D是AB的中垂线与圆的交点时,四边形DACB面积最大
此时△DAB为等边三角形,此时DC应为圆的直径,∠DAC=90°
∵∠ADC=∠BAC=30°,
∴DC=2AC=2,
∴四边形DACB的最大面积=
×
×2=
.
 解:(1)画图如图,∠DCE=∠A.
解:(1)画图如图,∠DCE=∠A.证明:∵四边形ABCD是圆内接四边形,
∴∠A+∠BCD=180°,
∴∠DCE+∠BCD=180°
∠DCE=∠A;
(2)AB=AC,
证明:∵四边形ABCD是圆内接四边形,
∴∠2=∠ABC,
∵∠1=∠ADB,∠ADB=∠ACB,
∴∠1=∠ACB,
∵DE平分∠FDC,
∴∠1=∠2,
∴∠ABC=∠ACB,
∴AB=AC;
(3)∵DC平分∠ADB,
∴∠ADC=∠BDC,
又∵∠ADC=∠ABC,∠BDC=∠BAC,
∴∠ABC=∠BAC,
∴AC=BC,
∵AB=
| 3 |
∴AC=BC=1,
∵S四边形DACB=S△ABC+S△DAB
S△ABC为定值,当S△DAB最大时,四边形DACB面积最大,
要使四边形DACB面积最大,只需求出面积最大的△DAB 即可
在△DAB中,AB边不变,当点D是AB的中垂线与圆的交点时,四边形DACB面积最大
此时△DAB为等边三角形,此时DC应为圆的直径,∠DAC=90°
∵∠ADC=∠BAC=30°,
∴DC=2AC=2,
∴四边形DACB的最大面积=
| 1 |
| 2 |
| 3 |
| 3 |
点评:本题考查的是圆的综合题,熟知圆内接四边形的性质、直角三角形的性质等知识是解答此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,已知△ABC,以AB、AC为边向外作正方形ABFD和正方形ACGE.连接BE,CD.BE与CD有什么数量关系?简单说明理由.
如图,已知△ABC,以AB、AC为边向外作正方形ABFD和正方形ACGE.连接BE,CD.BE与CD有什么数量关系?简单说明理由.