题目内容
19.如图,抛物线y=ax2+bx(a≠0)经过点A(2,0),点B(3,3),BC⊥x轴于点C,连接OB,等腰直角三角形DEF的斜边EF在x轴上,点E的坐标为(-4,0),点F与原点重合(1)求抛物线的解析式并直接写出它的对称轴;
(2)△DEF以每秒1个单位长度的速度沿x轴正方向移动,运动时间为t秒,当点D落在BC边上时停止运动,设△DEF与△OBC的重叠部分的面积为S,求出S关于t的函数关系式;
(3)点P是抛物线对称轴上一点,当△ABP是直角三角形时,请直接写出所有符合条件的点P坐标.
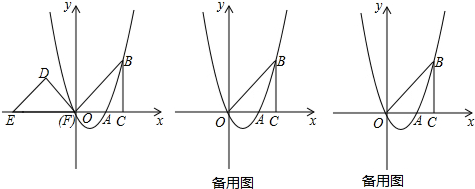
分析 (1)根据待定系数法解出解析式和对称轴即可;
(2)从三种情况分析①当0≤t≤3时,△DEF与△OBC重叠部分为等腰直角三角形;②当3<t≤4时,△DEF与△OBC重叠部分是四边形;③当4<t≤5时,△DEF与△OBC重叠部分是四边形得出S关于t的函数关系式即可;
(3)直接写出当△ABP是直角三角形时符合条件的点P坐标.
解答 解:(1)根据题意得$\left\{\begin{array}{l}0=4a+2b\\ 3=9a+3b\end{array}\right.$,
解得a=1,b=-2,
∴抛物线解析式是y=x2-2x,
对称轴是直线x=1;
(2)有3中情况:
①当0≤t≤3时,△DEF与△OBC重叠部分为等腰直角三角形,如图1: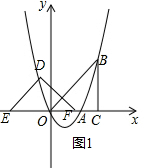
S=$\frac{1}{4}{t}^{2}$;
②当3<t≤4时,△DEF与△OBC重叠部分是四边形,如图2: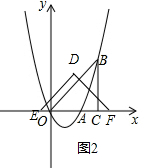
S=$-\frac{1}{4}{t}^{2}+3t-\frac{9}{2}$;
③当4<t≤5时,△DEF与△OBC重叠部分是四边形,如图3: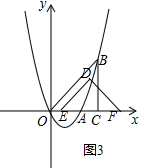
S=$-\frac{1}{2}{t}^{2}+3t-\frac{1}{2}$;
(3)当△ABP是直角三角形时,可得符合条件的点P坐标为(1,1)或(1,2)或(1,$\frac{1}{3}$)或(1,$\frac{11}{3}$).
点评 此题考查了难度较大的函数与几何的综合题,关键是根据0≤t≤3,3<t≤4,4<t≤5三种情况进行分析.

练习册系列答案
 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目
10. 在△ABC中,D、E为边AB、AC的中点,已知△ADE的面积为4,那么△ABC的面积是( )
在△ABC中,D、E为边AB、AC的中点,已知△ADE的面积为4,那么△ABC的面积是( )
 在△ABC中,D、E为边AB、AC的中点,已知△ADE的面积为4,那么△ABC的面积是( )
在△ABC中,D、E为边AB、AC的中点,已知△ADE的面积为4,那么△ABC的面积是( )| A. | 8 | B. | 12 | C. | 16 | D. | 20 |
14.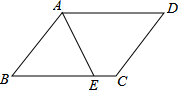 如图,?ABCD的周长为20cm,AE平分∠BAD,若CE=2cm,则AB的长度是( )
如图,?ABCD的周长为20cm,AE平分∠BAD,若CE=2cm,则AB的长度是( )
 如图,?ABCD的周长为20cm,AE平分∠BAD,若CE=2cm,则AB的长度是( )
如图,?ABCD的周长为20cm,AE平分∠BAD,若CE=2cm,则AB的长度是( )| A. | 10cm | B. | 8cm | C. | 6cm | D. | 4cm |
4. 如图,在?ABCD中,O是对角线AC,BD的交点,下列结论错误的是( )
如图,在?ABCD中,O是对角线AC,BD的交点,下列结论错误的是( )
 如图,在?ABCD中,O是对角线AC,BD的交点,下列结论错误的是( )
如图,在?ABCD中,O是对角线AC,BD的交点,下列结论错误的是( )| A. | AB∥CD | B. | AB=CD | C. | AC=BD | D. | OA=OC |
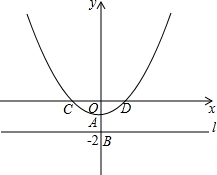 如图,在平面直角坐标系xOy中,直线l⊥y轴于点B(0,-2),A为OB的中点,以A为顶点的抛物线y=ax2+c与x轴交于C、D两点,且CD=4,点P为抛物线上的一个动点,以P为圆心,PO为半径画圆.
如图,在平面直角坐标系xOy中,直线l⊥y轴于点B(0,-2),A为OB的中点,以A为顶点的抛物线y=ax2+c与x轴交于C、D两点,且CD=4,点P为抛物线上的一个动点,以P为圆心,PO为半径画圆.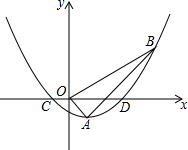 如图,在平面直角坐标系中,顶点为A(1,-1)的抛物线经过点B(5,3),且与x轴交于C,D两点(点C在点D的左侧).
如图,在平面直角坐标系中,顶点为A(1,-1)的抛物线经过点B(5,3),且与x轴交于C,D两点(点C在点D的左侧).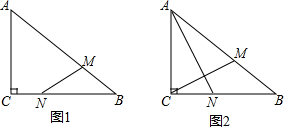
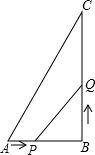 如图所示,在△ABC中∠B=90°,AB=6cm,BC=8cm,点P从点A开始沿AB边向点B以1cm/s的速度运动,点Q从点B开始沿BC边向点C以2cm/s的速度运动.
如图所示,在△ABC中∠B=90°,AB=6cm,BC=8cm,点P从点A开始沿AB边向点B以1cm/s的速度运动,点Q从点B开始沿BC边向点C以2cm/s的速度运动.