题目内容
12.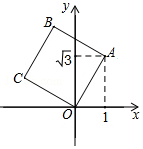 如图,将正方形OABC放在平面直角坐标系中,O是原点,A的坐标为(1,$\sqrt{3}$),则点B的坐标为( )
如图,将正方形OABC放在平面直角坐标系中,O是原点,A的坐标为(1,$\sqrt{3}$),则点B的坐标为( )| A. | (1-$\sqrt{3}$,$\sqrt{3}$+1) | B. | (-$\sqrt{3}$,$\sqrt{3}$+1) | C. | (-1,$\sqrt{3}$+1) | D. | (-1,$\sqrt{3}$) |
分析 作AE⊥x轴于E,BF⊥EA交EA的延长线于F,BF交y轴于H.则易知四边形OEFH是矩形.只要证明△BAF≌△AOE,推出BF=AE=$\sqrt{3}$,AF=OE=1,推出BH=$\sqrt{3}$-1,EF=1+$\sqrt{3}$,由此即可解决问题.
解答 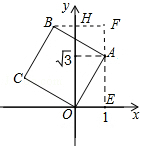 解:作AE⊥x轴于E,BF⊥EA交EA的延长线于F,BF交y轴于H.则易知四边形OEFH是矩形.
解:作AE⊥x轴于E,BF⊥EA交EA的延长线于F,BF交y轴于H.则易知四边形OEFH是矩形.
∵四边形ABCO是正方形,A(1,$\sqrt{3}$),
∴AB=AO,∠BAO=90°,AE=$\sqrt{3}$,HF=OE=1,∠BFA=∠AEO=90°,
∴∠BAF+∠OAE=90°,∠OAE+∠AOE=90°,
∴∠BAF=∠AOE,
在△BAF和△AOE中,
$\left\{\begin{array}{l}{∠BAF=∠AOE}\\{∠F=∠AEO}\\{AB=OA}\end{array}\right.$,
∴△BAF≌△AOE,
∴BF=AE=$\sqrt{3}$,AF=OE=1,
∴BH=$\sqrt{3}$-1,EF=1+$\sqrt{3}$,
∵B在第三象限,
∴B(1-$\sqrt{3}$,1+$\sqrt{3}$).
故选A.
点评 本题考查了全等三角形的判定与性质,正方形的性质,坐标与图形性质,作辅助线构造出全等三角形是解题的关键,也是本题的难点.

练习册系列答案
相关题目
2.把点A(2,-3)先向上平移2个单位,再向左平移3个单位得到的点的坐标为( )
| A. | (4,0) | B. | (-1,-1) | C. | (5,-1) | D. | (-1,-5) |
20.有理数中,比-3大2的数是( )
| A. | -5 | B. | 5 | C. | 1 | D. | -1 |
7.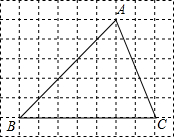 在正方形网格中,△ABC的位置如图所示,则cos∠B的值为( )
在正方形网格中,△ABC的位置如图所示,则cos∠B的值为( )
 在正方形网格中,△ABC的位置如图所示,则cos∠B的值为( )
在正方形网格中,△ABC的位置如图所示,则cos∠B的值为( )| A. | $\frac{\sqrt{2}}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | 1 |
17.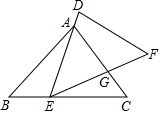 如图,已知△ABC和△DEF,点E在BC边上,点A在DE边上,边EF和边AC相交于点G.如果AE=EC,∠AEG=∠B,那么添加下列一个条件后,仍无法判定△DEF与△ABC一定相似的是( )
如图,已知△ABC和△DEF,点E在BC边上,点A在DE边上,边EF和边AC相交于点G.如果AE=EC,∠AEG=∠B,那么添加下列一个条件后,仍无法判定△DEF与△ABC一定相似的是( )
 如图,已知△ABC和△DEF,点E在BC边上,点A在DE边上,边EF和边AC相交于点G.如果AE=EC,∠AEG=∠B,那么添加下列一个条件后,仍无法判定△DEF与△ABC一定相似的是( )
如图,已知△ABC和△DEF,点E在BC边上,点A在DE边上,边EF和边AC相交于点G.如果AE=EC,∠AEG=∠B,那么添加下列一个条件后,仍无法判定△DEF与△ABC一定相似的是( )| A. | $\frac{AB}{BC}$=$\frac{DE}{EF}$ | B. | $\frac{AD}{AE}$=$\frac{GF}{GE}$ | C. | $\frac{AG}{AC}$=$\frac{EG}{EF}$ | D. | $\frac{ED}{EF}$=$\frac{EG}{EA}$ |
4.-$\frac{1}{2}$的相反数是( )
| A. | $\frac{1}{2}$ | B. | 2 | C. | -0.5 | D. | -2 |
1.下面式子是二次根式的是( )
| A. | $\sqrt{{a}^{2}+1}$ | B. | $\root{3}{33}$ | C. | $\sqrt{-1}$ | D. | $\frac{1}{2}$a |
2.已知m-n=7,mn=8,则(m+n)2的值为( )
| A. | 81 | B. | 64 | C. | 17 | D. | 15 |