题目内容
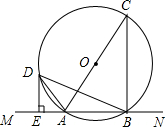 已知:如图,直线MN交⊙O于A、B两点,AC是直径,D为⊙O上一点,过D作DE⊥MN于E,DE是⊙O的切线.
已知:如图,直线MN交⊙O于A、B两点,AC是直径,D为⊙O上一点,过D作DE⊥MN于E,DE是⊙O的切线.(1)求证:AD平分∠CAM;
(2)若⊙O的半径为7.5cm,AE=3cm,求tan∠CBD的值.
考点:切线的性质
专题:
分析:(1)由DE与圆O相切,利用切线的性质得到∠ADE=∠ABD,再根据直角三角形的性质得出∠ABD+∠BDE=90°,∠ADE+∠DAE=90°,从而得出∠BDE=∠DAE,利用圆周角的性质,得到BC⊥MN,进而求得DE∥BC,利用两直线平行得到一对内错角相等,得出∠DAE=∠DAC,即AD为∠CAE的平分线;
(2)连接OD,过O作OF⊥AB,显然得到四边形ODEF为矩形,利用矩形的对边相等得到OD=EF,OF=DE,设DE=x,由EF-AE=OD-EF表示出AF的长,在直角三角形AOF中,利用勾股定理列出关于x的方程,求出方程的解即可得到DE的长,然后通过解直角三角形即可求得tan∠CBD的值.
(2)连接OD,过O作OF⊥AB,显然得到四边形ODEF为矩形,利用矩形的对边相等得到OD=EF,OF=DE,设DE=x,由EF-AE=OD-EF表示出AF的长,在直角三角形AOF中,利用勾股定理列出关于x的方程,求出方程的解即可得到DE的长,然后通过解直角三角形即可求得tan∠CBD的值.
解答:(1)证明:∵DE切圆O于D,
∴∠ADE=∠ABD,
又∵DE⊥MN,
∴∠DEB=90°,
∴∠ABD+∠BDE=90°,∠ADE+∠DAE=90°
∴∠BDE=∠DAE,
∵AC是直径,
∴BC⊥MN,
∴DE∥BC,
∴∠BDE=∠DBC,
又∵∠DAC=∠DBC,
∴∠DAC=∠DAE,
∴AD平分∠CAM;
(2)解:连接OD,过O作OF⊥AB,
∵DE是⊙O的切线.
∴OD⊥DE,
∴四边形ODEF为矩形,
∴OF=DE,OD=EF,
设DE=xcm,AE=3cm,OD=EF=OA=7.5cm,
∴AF=EF-AE=(7.5-3)=4.5cm,
在Rt△AOF中,根据勾股定理得:OA2=AF2+OF2,即7.52=4.52+x2,
解得:x=6cm.
∴DE=6cm,
∴∠DAE=∠CBD,
∴tan∠CBD=tan∠DAE=
=
=2.
∴∠ADE=∠ABD,
又∵DE⊥MN,
∴∠DEB=90°,
∴∠ABD+∠BDE=90°,∠ADE+∠DAE=90°
∴∠BDE=∠DAE,
∵AC是直径,
∴BC⊥MN,
∴DE∥BC,
∴∠BDE=∠DBC,
又∵∠DAC=∠DBC,
∴∠DAC=∠DAE,
∴AD平分∠CAM;
(2)解:连接OD,过O作OF⊥AB,
∵DE是⊙O的切线.

∴OD⊥DE,
∴四边形ODEF为矩形,
∴OF=DE,OD=EF,
设DE=xcm,AE=3cm,OD=EF=OA=7.5cm,
∴AF=EF-AE=(7.5-3)=4.5cm,
在Rt△AOF中,根据勾股定理得:OA2=AF2+OF2,即7.52=4.52+x2,
解得:x=6cm.
∴DE=6cm,
∴∠DAE=∠CBD,
∴tan∠CBD=tan∠DAE=
| DE |
| AE |
| 6 |
| 3 |
点评:此题考查了切线的性质,勾股定理,平行线的判定与性质,解直角三角形等,利用了转化及方程的思想,熟练掌握切线的性质是解本题的关键.

练习册系列答案
 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目
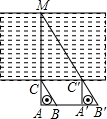 如图,一名同学拿一把含30°角直角三角尺ABC(即∠ACB=30°)目测一条河的宽度,他先在岸边点A处顺着30°角的邻边AC的方向看见河对岸的一棵树M,然后沿30°角的对边AB的方向前进到B′处,顺着斜边B′C′的方向看见树M,并测得AA′=100米,则他目测的河宽MC大约是多少米(精确到1米)?
如图,一名同学拿一把含30°角直角三角尺ABC(即∠ACB=30°)目测一条河的宽度,他先在岸边点A处顺着30°角的邻边AC的方向看见河对岸的一棵树M,然后沿30°角的对边AB的方向前进到B′处,顺着斜边B′C′的方向看见树M,并测得AA′=100米,则他目测的河宽MC大约是多少米(精确到1米)? 如图所示,已知点O是AB中点,且AP=28cm,点P是AB上一点,点AP:PB=5:2,则OP=
如图所示,已知点O是AB中点,且AP=28cm,点P是AB上一点,点AP:PB=5:2,则OP=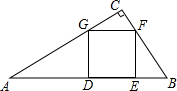 如图,在Rt△ABC中,∠C=90°,正方形DEFG的顶点D,E在AB边上,F,G分别在BC和AC上.
如图,在Rt△ABC中,∠C=90°,正方形DEFG的顶点D,E在AB边上,F,G分别在BC和AC上. 如图,在梯形ABCD中,AD∥BC,AE平分∠BAD,BE平分∠ABC,且AE、BE交CD于点E.试说明AD=AB-BC的理由.
如图,在梯形ABCD中,AD∥BC,AE平分∠BAD,BE平分∠ABC,且AE、BE交CD于点E.试说明AD=AB-BC的理由.