题目内容
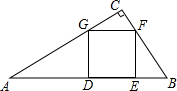 如图,在Rt△ABC中,∠C=90°,正方形DEFG的顶点D,E在AB边上,F,G分别在BC和AC上.
如图,在Rt△ABC中,∠C=90°,正方形DEFG的顶点D,E在AB边上,F,G分别在BC和AC上.(1)证明:△ADG∽△FEB.
(2)若AD=4,BE=2,求:正方形DEFG的边长.
考点:相似三角形的判定与性质,正方形的性质
专题:
分析:(1)易证∠AGD=∠B,根据∠ADG=∠BEF=90°,即可证明△ADG∽△FEB;
(2)根据(1)中结论可得
=
,根据DG=EF即可求得EF的长,即可解题.
(2)根据(1)中结论可得
| AD |
| DG |
| EF |
| BE |
解答:(1)证明:∵∠A+∠AGD=90°,∠A+∠B=90°,
∴∠AGD=∠B,
∵∠ADG=∠BEF=90°,
∴△ADG∽△FEB;
(2)解:∵△ADG∽△FEB,
∴
=
,
∵EF=DG,
∴EF•EF=AD•BE=8,
∴EF=2
.
∴∠AGD=∠B,
∵∠ADG=∠BEF=90°,
∴△ADG∽△FEB;
(2)解:∵△ADG∽△FEB,
∴
| AD |
| DG |
| EF |
| BE |
∵EF=DG,
∴EF•EF=AD•BE=8,
∴EF=2
| 2 |
点评:本题考查了相似三角形的判定,考查了相似三角形对应边比例相等的性质,本题中求证△ADG∽△FEB是解题的关键.

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
 如图,AB为⊙O的直径,DE是⊙O的切线,⊙O过BC上一点D,过D作DE⊥AC于E点,求证:BD=CD.
如图,AB为⊙O的直径,DE是⊙O的切线,⊙O过BC上一点D,过D作DE⊥AC于E点,求证:BD=CD.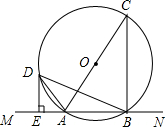 已知:如图,直线MN交⊙O于A、B两点,AC是直径,D为⊙O上一点,过D作DE⊥MN于E,DE是⊙O的切线.
已知:如图,直线MN交⊙O于A、B两点,AC是直径,D为⊙O上一点,过D作DE⊥MN于E,DE是⊙O的切线.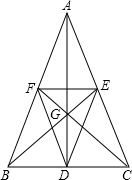 如图,AD、BE、CF是△ABC的中线,G是△ABC的重心.△DEF与△ABC是位似图形吗?并说明理由.
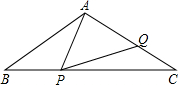
如图,AD、BE、CF是△ABC的中线,G是△ABC的重心.△DEF与△ABC是位似图形吗?并说明理由.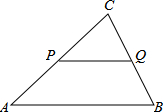 如图,在△ABC中,PQ∥AB,AC=3,若S△PQC=S四边形PABQ,试求CP的长.
如图,在△ABC中,PQ∥AB,AC=3,若S△PQC=S四边形PABQ,试求CP的长.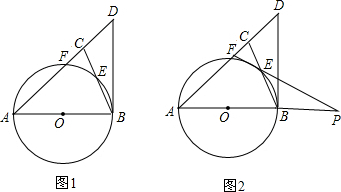
 如图,在等腰△ABC中,AB=AC=6cm,BC=10cm,点P从点B出发,以2cm/s的速度沿BC向点C运动,设点P的运动时间为t s.
如图,在等腰△ABC中,AB=AC=6cm,BC=10cm,点P从点B出发,以2cm/s的速度沿BC向点C运动,设点P的运动时间为t s.