题目内容
已知线段AB上有P、Q两点,AB=26,AP=14,PQ=11,点C是线段AB的中点,求线段CQ的长.
考点:两点间的距离
专题:计算题
分析:先根据线段中点的定义得到AC=
AB=13,则利用PC=AP-AC计算出PC,然后利用CQ=CP+PQ进行计算即可.
| 1 |
| 2 |
解答:解:如图,
∵点C是线段AB的中点,
∴AC=
AB=13,
∴PC=AP-AC=14-13=1,
∴CQ=CP+PQ=1+11=12,
即CQ的长为12.

∵点C是线段AB的中点,
∴AC=
| 1 |
| 2 |
∴PC=AP-AC=14-13=1,
∴CQ=CP+PQ=1+11=12,
即CQ的长为12.
点评:本题考查了两点间的距离:连接两点间的线段的长度叫两点间的距离.距离是一个量,有大小,区别于线段,线段是图形.线段的长度才是两点的距离.可以说画线段,但不能说画距离.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
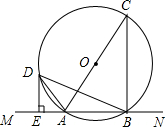 已知:如图,直线MN交⊙O于A、B两点,AC是直径,D为⊙O上一点,过D作DE⊥MN于E,DE是⊙O的切线.
已知:如图,直线MN交⊙O于A、B两点,AC是直径,D为⊙O上一点,过D作DE⊥MN于E,DE是⊙O的切线.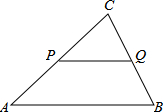 如图,在△ABC中,PQ∥AB,AC=3,若S△PQC=S四边形PABQ,试求CP的长.
如图,在△ABC中,PQ∥AB,AC=3,若S△PQC=S四边形PABQ,试求CP的长. 已知:线段AB=a,M是AB的中点,C是AM的中点,D是CB的中点,求MD的长.
已知:线段AB=a,M是AB的中点,C是AM的中点,D是CB的中点,求MD的长.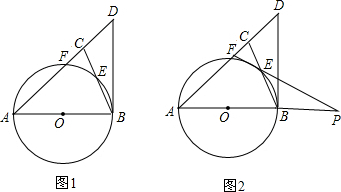
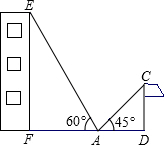 如图,在一次课外数学实践活动中,小明站在操场的A处,他的两侧分别是旗杆CD和一幢教学楼EF,点A、D、F在同一直线上,从A处测得旗杆顶部和教学楼顶部的仰角分别为45°和60°,已知DF=16m,EF=18m,求旗杆CD高.(结果精确到0.1m,参考数据:
如图,在一次课外数学实践活动中,小明站在操场的A处,他的两侧分别是旗杆CD和一幢教学楼EF,点A、D、F在同一直线上,从A处测得旗杆顶部和教学楼顶部的仰角分别为45°和60°,已知DF=16m,EF=18m,求旗杆CD高.(结果精确到0.1m,参考数据: