题目内容
平面直角坐标系中A(1,4),B(4,1).
(1)动点P在x轴上,且P到A、B的距离之和最小,求点P的坐标.
(2)若动点P在y轴,当△ABQ周长最小时,求点Q的坐标.
(3)若x轴上有一点P,y轴上有一点Q,四边形ABPQ的周长是否存在最小?若有请求之,若无请说明理由.
(1)动点P在x轴上,且P到A、B的距离之和最小,求点P的坐标.
(2)若动点P在y轴,当△ABQ周长最小时,求点Q的坐标.
(3)若x轴上有一点P,y轴上有一点Q,四边形ABPQ的周长是否存在最小?若有请求之,若无请说明理由.
考点:轴对称-最短路线问题,坐标与图形性质
专题:
分析:(1)作A关于x轴的对称点C,连接BC交x轴于P,则此时AP+BP最小,求出C的坐标,设直线BC的解析式是y=kx+b,把B、C的坐标代入求出k、b,得出直线BC的解析式,求出直线与x轴的交点坐标即可.
(2)首先作点A关于y轴的对称点D连接DB,DB与y轴交点即为Q点,则此时△ABQ周长最小,求出过D,B两点的直线函数关系式,再求出直线与y轴交点坐标即可;
(3)作A点关于y轴对称点A′,作B点关于x轴对称点B′,进而连接A′B′,交y轴于点Q,交x轴于点P,此时四边形ABPQ的周长最小,利用勾股定理即可得出答案.
(2)首先作点A关于y轴的对称点D连接DB,DB与y轴交点即为Q点,则此时△ABQ周长最小,求出过D,B两点的直线函数关系式,再求出直线与y轴交点坐标即可;
(3)作A点关于y轴对称点A′,作B点关于x轴对称点B′,进而连接A′B′,交y轴于点Q,交x轴于点P,此时四边形ABPQ的周长最小,利用勾股定理即可得出答案.
解答: 解:(1)如图1,作A关于x轴的对称点C,连接BC交x轴于P,则此时AP+BP最小,
解:(1)如图1,作A关于x轴的对称点C,连接BC交x轴于P,则此时AP+BP最小,
∵A点的坐标为(1,4),B点的坐标为(4,1),
∴C(1,-4),
设直线BC的解析式是:y=kx+b,
把B、C的坐标代入得:
,
解得
.
即直线BC的解析式是y=
x-
,
当y=0时,
x-
=0,
解得:x=
,
∴P点的坐标是(
,0).
(2)如图2,作点A关于y轴的对称点D(-1,4),连接DB,DB与y轴交点即为Q点,则此时△ABQ周长最小;
设过D,B两点的直线函数关系式为y=mx+n,
∵D(-1,4).B(4,1),
∴
,
解得:
,
∴过D,B两点的直线函数关系式为y=-
x+
;
当x=0时,y=
,
即:直线DB与y轴交于点(0,
),
∴Q点坐标是(0,
).
(3)如图3:作A点关于y轴对称点A′,作B点关于x轴对称点B′,进而连接A′B′,交y轴于点Q,交x轴于点P,此时四边形ABPQ的周长最小,
∵A点的坐标是(1,4),B点的坐标是(4,1),
∴AB=
=3
,A′(-1,4),B′(4,-1),
故A′B′=
=5
,
则四边形PABQ的周长最短的值为:3
+5
=8
.

 解:(1)如图1,作A关于x轴的对称点C,连接BC交x轴于P,则此时AP+BP最小,
解:(1)如图1,作A关于x轴的对称点C,连接BC交x轴于P,则此时AP+BP最小,∵A点的坐标为(1,4),B点的坐标为(4,1),
∴C(1,-4),
设直线BC的解析式是:y=kx+b,
把B、C的坐标代入得:
|
解得
|
即直线BC的解析式是y=
| 5 |
| 3 |
| 17 |
| 3 |
当y=0时,
| 5 |
| 3 |
| 17 |
| 3 |
解得:x=
| 17 |
| 5 |
∴P点的坐标是(
| 17 |
| 5 |
(2)如图2,作点A关于y轴的对称点D(-1,4),连接DB,DB与y轴交点即为Q点,则此时△ABQ周长最小;

设过D,B两点的直线函数关系式为y=mx+n,
∵D(-1,4).B(4,1),
∴
|
解得:
|
∴过D,B两点的直线函数关系式为y=-
| 3 |
| 5 |
| 17 |
| 5 |
当x=0时,y=
| 17 |
| 5 |
即:直线DB与y轴交于点(0,
| 17 |
| 5 |
∴Q点坐标是(0,
| 17 |
| 5 |
(3)如图3:作A点关于y轴对称点A′,作B点关于x轴对称点B′,进而连接A′B′,交y轴于点Q,交x轴于点P,此时四边形ABPQ的周长最小,
∵A点的坐标是(1,4),B点的坐标是(4,1),
∴AB=
| (1-4)2+(4-1)2 |
| 2 |
故A′B′=
| (-1-4)2+(4+1)2 |
| 2 |
则四边形PABQ的周长最短的值为:3
| 2 |
| 2 |
| 2 |

点评:本题考查了一次函数图象上点的坐标特征,用待定系数法求一次函数的解析式,轴对称-最短路线问题的应用,关键是能找出P、Q点,题目具有一定的代表性,难度适中.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
下列运算正确的是( )
A、
| ||||||||||
B、
| ||||||||||
C、
| ||||||||||
D、
|
 (1)解不等式
(1)解不等式
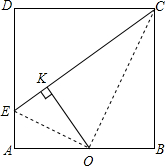 如图,在正方形ABCD的一边上取一点E,使AE=
如图,在正方形ABCD的一边上取一点E,使AE=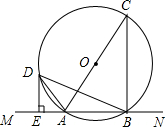 已知:如图,直线MN交⊙O于A、B两点,AC是直径,D为⊙O上一点,过D作DE⊥MN于E,DE是⊙O的切线.
已知:如图,直线MN交⊙O于A、B两点,AC是直径,D为⊙O上一点,过D作DE⊥MN于E,DE是⊙O的切线.