题目内容
4．
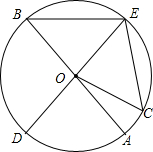如图，AB，DE是⊙O的直径，C是⊙O上的一点，且$\widehat{AD}$=$\widehat{CE}$．（1）求证：BE=CE；
（2）若∠B=50°，求∠AOC的度数．
分析 （1）根据∠AOD=∠BOE可知$\widehat{AD}$=$\widehat{BE}$，再由$\widehat{AD}$=$\widehat{CE}$即可得出结论；
（2）先根据等腰三角形的性质求出∠BOE的度数，再由BE=CE可得出∠BOE=∠COE，根据补角的定义即可得出结论．
解答 （1）证明：∵∠AOD=∠BOE，
∴$\widehat{AD}$=$\widehat{BE}$．
∵$\widehat{AD}$=$\widehat{CE}$，
∴$\widehat{BE}$=$\widehat{CE}$，
∴BE=CE；
（2）解：∵∠B=50°，OB=OE，
∴∠BOE=180°-50°-50°=80°．
∵由（1）知，BE=CE，
∴∠COE=∠BOE=80°，
∴∠AOC=180°-80°-80°=20°．
点评 本题考查的是圆心角、弧、弦的关系，熟知在同圆或等圆中，如果两个圆心角、两条弧、两条弦中有一组量相等，那么它们所对应的其余各组量都分别相等是解答此题的关键．
练习册系列答案
相关题目
转动如图所示的转盘两次．两次所得的颜色相同的概率是多少？
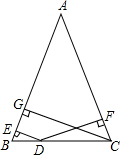如图，已知△ABC中，AB=AC，D是底边BC上任意一点，DB=DC，DE⊥AB，DF⊥AC，CG⊥AB，求证：DE+DF=CG．
如图，△ABC中，DE∥BC，AN交DE于M，求证：$\frac{DM}{BN}=\frac{EM}{CN}$．