题目内容
14.已知$\frac{x}{y}$=$\frac{a}{b}$=$\frac{c}{d}$=$\frac{3}{2}$(y+b+d≠0),则$\frac{x+2a-3c}{y+2b-3d}$=$\frac{3}{2}$.(y+2b-3d≠0)分析 根据比的性质,可得$\frac{x}{y}$=$\frac{2a}{2b}$=$\frac{3c}{3d}$=$\frac{3}{2}$,根据等比性质,可得答案.
解答 解:由比的性质,得
$\frac{x}{y}$=$\frac{2a}{2b}$=$\frac{3c}{3d}$=$\frac{3}{2}$,
由等比性质,得
$\frac{x+2a-3c}{y+2b-3d}$=$\frac{3}{2}$,
故答案为:$\frac{3}{2}$.
点评 本题考查了比例的性质,利用了比的性质:比的前项与后项都乘以(或除以)相同的倍数,比值不变,又利用了等比性质.

练习册系列答案
相关题目
6.多项式2x2-x+1的各项分别是( )
| A. | 2x2,x,1 | B. | 2x2,-x,1 | C. | -2x2,x,-1 | D. | -2x2,-x,-1 |
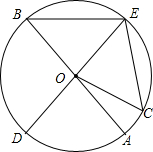 如图,AB,DE是⊙O的直径,C是⊙O上的一点,且$\widehat{AD}$=$\widehat{CE}$.
如图,AB,DE是⊙O的直径,C是⊙O上的一点,且$\widehat{AD}$=$\widehat{CE}$.