题目内容
3.解方程或不等式组:(1)$\frac{2}{x-1}$-$\frac{1}{x+1}$=$\frac{3}{{x}^{2}-1}$.
(2)$\left\{\begin{array}{l}{5x-3≥2x}\\{\frac{3x-1}{2}<4}\end{array}\right.$.
分析 (1)分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解;
(2)分别求出不等式组中两不等式的解集,找出解集的公共部分即可确定出不等式组的解集.
解答 解:(1)方程两边都乘以最简公分母(x+1)(x-1),得:2(x+1)-(x-1)=3,
解得:x=0,
检验:将x=0代入(x+1)(x-1)中,得(0+1)(0-1)=-1≠0,
∴x=0是原方程的解;
(2)$\left\{\begin{array}{l}{5x-3≥2x①}\\{\frac{3x-1}{2}<4②}\end{array}\right.$,
解不等式①得:x≥1;
解不等式②得:x<3,
则原不等式组的解集是1≤x<3.
点评 此题考查了解分式方程,以及解一元一次不等式组,熟练掌握运算法则是解本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
14.在Rt△ABC中,∠C=90°,AB=4,AC=1,则tanA的值是( )
| A. | $\frac{{\sqrt{15}}}{4}$ | B. | $\sqrt{15}$ | C. | $\frac{1}{4}$ | D. | 4 |
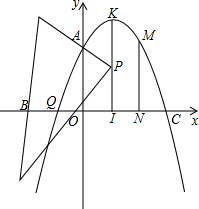 如图,已知抛物线y=ax2+bx+3经过点B(-1,0)、C(3,0),交y轴于点A,
如图,已知抛物线y=ax2+bx+3经过点B(-1,0)、C(3,0),交y轴于点A, 在平面直角坐标系xOy中,定义直线y=ax+b为抛物线y=ax2+bx的特征直线,C(a,b)为其特征点.设抛物线y=ax2+bx与其特征直线交于A、B两点(点A在点B的左侧).
在平面直角坐标系xOy中,定义直线y=ax+b为抛物线y=ax2+bx的特征直线,C(a,b)为其特征点.设抛物线y=ax2+bx与其特征直线交于A、B两点(点A在点B的左侧).