题目内容
14.如图,四边形ABCD是正方形,点E在BC上,过D点作DG⊥DE交BA的延长线于G.(1)求证:DE=DG;
(2)以线段DE、DG为边作出正方形DEFG,点K在AB上且BK=AG,连接KF,请画出图形,猜想四边形CEFK是怎样的特殊四边形,并证明你的猜想;
(3)当$\frac{CE}{CB}=\frac{m}{n}$时,请直接写出$\frac{{S}_{正方形ABCD}}{{S}_{正方形DEFG}}$的值.
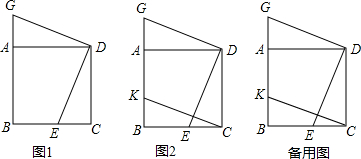
分析 (1)由已知证明DE、DG所在的三角形全等,再通过等量代换证明DE⊥DG;
(2)根据正方形的性质分别以点G、E为圆心以DG为半径画弧交点F,得到正方形DEFG,由已知首先证四边形CKGD是平行四边形,然后证明四边形CEFK为平行四边形;
(3)由$\frac{CE}{CB}=\frac{m}{n}$,设CE=mx,CB=nx,于是得到CD=nx,根据勾股定理得到DE2=CE2+CD2=n2x2+m2x2=(n2+m2)x2,由于BC2=n2x2,即可得到结论;
解答 (1)证明:∵四边形ABCD是正方形,
∴DC=DA,∠DCE=∠DAG=90°.
在△DCE与△DAG中,$\left\{\begin{array}{l}{CD=DA}\\{∠DCE=∠DAG}\\{CE=AG}\end{array}\right.$,
∴△DCE≌△DAG,
∴DE=DG;
(2)解:四边形CEFK为平行四边形.
证明:设CK、DE相交于M点,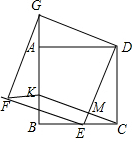
∵四边形ABCD和四边形DEFG都是正方形,
∴AB∥CD,AB=CD,EF=DG,EF∥DG,
∵BK=AG,
∴KG=AB=CD,
∴四边形CKGD是平行四边形,
∴CK=DG=EF,CK∥DG,
∴∠KME=∠GDE=∠DEF=90°,
∴∠KME+∠DEF=180°,
∴CK∥EF,
∴四边形CEFK为平行四边形.
(3)解:∵$\frac{CE}{CB}=\frac{m}{n}$,
∴设CE=mx,CB=nx,
∴CD=nx,
∴DE2=CE2+CD2=n2x2+m2x2=(n2+m2)x2,
∵BC2=n2x2,
∴$\frac{{S}_{正方形ABCD}}{{S}_{正方形DEFG}}$=$\frac{B{C}^{2}}{D{E}^{2}}$=$\frac{{n}^{2}}{{m}^{2}+{n}^{2}}$.
点评 此题考查的知识点是正方形的性质、全等三角形的判定和性质、平行四边形的判定及作图,解题的关键是先由正方形的性质通过证三角形全等得出结论,此题较复杂.

| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
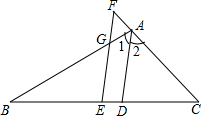 如图,在△ABC中,AD平分∠BAC,E为BC的中点,过点E作EF∥AD交AB于点G,交CA的延长线于点F.求证:BG=CF.
如图,在△ABC中,AD平分∠BAC,E为BC的中点,过点E作EF∥AD交AB于点G,交CA的延长线于点F.求证:BG=CF.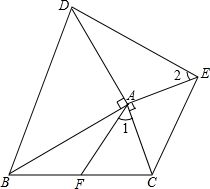 将两块等腰直角三角板△ABD,△ACE如图摆放,0°<∠BAC<180°,连接BC,DE,AF是△ABC的中线.求证:
将两块等腰直角三角板△ABD,△ACE如图摆放,0°<∠BAC<180°,连接BC,DE,AF是△ABC的中线.求证: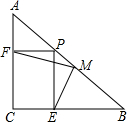 已知:如图,在△ABC中,AC=BC,∠ACB=90°,在BA上任取一点P,PE⊥BC于E,PF⊥AC于F,M是AB的中点.证明:
已知:如图,在△ABC中,AC=BC,∠ACB=90°,在BA上任取一点P,PE⊥BC于E,PF⊥AC于F,M是AB的中点.证明: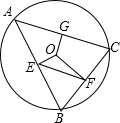 如图,⊙O的半径是7,△ABC是⊙O的内接三角形,过圆心O分别作AB、BC、AC的垂线段,垂足为E、F、G,连接EF.若OG=4,则EF为$\sqrt{33}$.
如图,⊙O的半径是7,△ABC是⊙O的内接三角形,过圆心O分别作AB、BC、AC的垂线段,垂足为E、F、G,连接EF.若OG=4,则EF为$\sqrt{33}$.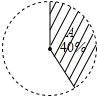 如图,扇形A的圆心角的度数为144°.
如图,扇形A的圆心角的度数为144°.