题目内容
9.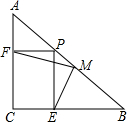 已知:如图,在△ABC中,AC=BC,∠ACB=90°,在BA上任取一点P,PE⊥BC于E,PF⊥AC于F,M是AB的中点.证明:
已知:如图,在△ABC中,AC=BC,∠ACB=90°,在BA上任取一点P,PE⊥BC于E,PF⊥AC于F,M是AB的中点.证明:(1)ME=MF;
(2)PF+BE=AC.
分析 (1)欲证明MF=ME,只要证明△AFM≌△CEM即可.
(2)欲证明PF+BE=AC,因为AC=AF+CF,所以只要证明PF=AF,EB=FC,利用矩形的性质.等腰三角形的性质即可证明.
解答 (1)证明:连接MC.
∵PE⊥BC,PF⊥AC,
∴∠PEC=∠PFC=∠=90°,
∴四边形PECF是矩形,
∴PF=EC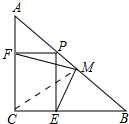
∵CA=CB,∠=90°,AM=MB,
∴CM=AM=MB,∠A=∠B=∠APF=∠ACM=∠MCB=45°,
∴AF=PF,
在△AFM和△CEM中,
$\left\{\begin{array}{l}{AM=CM}\\{∠A=∠MCB}\\{AF=CE}\end{array}\right.$,
∴△AFM≌△CEM,
∴FM=ME.
(2)∵四边形PECF是矩形,
∴PE=CF,
∵∠B=45°,∠PEB=90°,
∴∠B=∠EPB=45°,
∴PE=EB,
∵PF=AF,
∴PF+BE=AF+FC=AC.
点评 本题考查全等三角形的判定和性质、等腰三角形的性质、矩形的判定和性质等知识,添加辅助线构造全等三角形是解决问题的关键,属于中考常考题型.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1.下列说法正确的是( )
| A. | 经过两点可以画无数条直线 | |
| B. | 两条射线组成的图形叫做角 | |
| C. | 正多边形的各边都相等,各角都相等 | |
| D. | 两个锐角的和一定大于直角 |
18.线段CD是由线段AB平移得到的,点A(-1,4)的对应点为C(-1,7),则点B(-4,-1)的对应点D的坐标为( )
| A. | (2,9) | B. | (5,3) | C. | (-4,2) | D. | (-9,-4) |
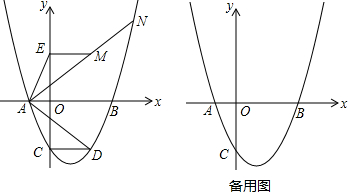
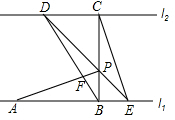 如图,已知直线l1∥l2,线段AB在直线l1上,BC垂直于l1交l2于点C,且AB=BC,P是线段BC上异于两端点的一点,过点P的直线分别交l2,l1于点D,E(点A,E位于点B的两侧),满足BP=BE,连接AP,CE.
如图,已知直线l1∥l2,线段AB在直线l1上,BC垂直于l1交l2于点C,且AB=BC,P是线段BC上异于两端点的一点,过点P的直线分别交l2,l1于点D,E(点A,E位于点B的两侧),满足BP=BE,连接AP,CE.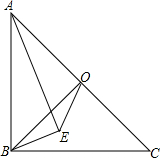 如图,在等腰Rt△ABC中,O为斜边AC的中点,连接BO,以AB为斜边向三角内部作Rt△ABE,且∠AEB=90°,连接EO.求证:
如图,在等腰Rt△ABC中,O为斜边AC的中点,连接BO,以AB为斜边向三角内部作Rt△ABE,且∠AEB=90°,连接EO.求证: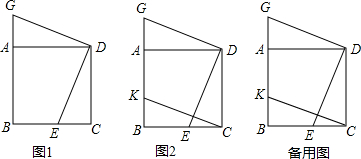
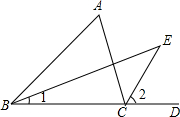 请在下列证明过程中,标注恰当的理由.如图,在△ABC中,∠ABC的平分线BE与∠ACD的平分线CE相交于点E.
请在下列证明过程中,标注恰当的理由.如图,在△ABC中,∠ABC的平分线BE与∠ACD的平分线CE相交于点E.