题目内容
2.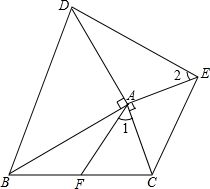 将两块等腰直角三角板△ABD,△ACE如图摆放,0°<∠BAC<180°,连接BC,DE,AF是△ABC的中线.求证:
将两块等腰直角三角板△ABD,△ACE如图摆放,0°<∠BAC<180°,连接BC,DE,AF是△ABC的中线.求证:(1)∠DAE+∠BAC=180°;
(2)∠1=∠2.
分析 (1)根据周角的定义即可得到结论;
(2)延长AF到G,使FG=AF,通过△ACF≌△BGF,根据全等三角形的性质得到BG=AC,∠G=∠1,∠FBG=∠ACF,求得∠ABG=∠DAE,推出△ABG≌△ADE,根据全等三角形的性质即可得到结论.
解答 证明:(1)∵∠BAD=∠CAE=90°,
∴∠DAE+∠BAC=360°-∠DAB-∠CAE=180°;
(2)延长AF到G,使FG=AF,
∵AF是△ABC的中线,
∴BF=CF,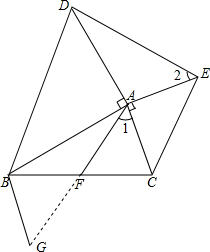
在△ACF与△BFG中,$\left\{\begin{array}{l}{AF=FG}\\{∠AFC=∠BFG}\\{CF=BF}\end{array}\right.$,
∴△ACF≌△BGF,
∴BG=AC,∠G=∠1,∠FBG=∠ACF,
∴∠ABG=180°-∠BAC,
∵∠DAE=180°-∠BAC,
∴∠ABG=∠DAE,
∵AE=AC,
∴AE=BG,
在△ABG与△ADE中,$\left\{\begin{array}{l}{AB=AD}\\{∠ABG=∠DAE}\\{BG=AE}\end{array}\right.$,
∴△ABG≌△ADE,
∴∠G=∠2,
∴∠1=∠2.
点评 本题考查了全等三角形的判定和性质,等腰直角三角形的性质,正确的作出辅助线构造全等三角形是解题的关键.

练习册系列答案
 全程金卷系列答案
全程金卷系列答案 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
8.-(x-3)去括号后正确的是( )
| A. | x-3 | B. | -x+3 | C. | x+3 | D. | -3-x |
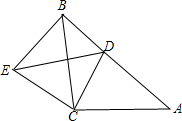 如图,△ABC与△CDE均是等腰直角三角形,∠ACB=∠DCE=90°,D在AB上,连接BE.
如图,△ABC与△CDE均是等腰直角三角形,∠ACB=∠DCE=90°,D在AB上,连接BE.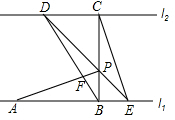 如图,已知直线l1∥l2,线段AB在直线l1上,BC垂直于l1交l2于点C,且AB=BC,P是线段BC上异于两端点的一点,过点P的直线分别交l2,l1于点D,E(点A,E位于点B的两侧),满足BP=BE,连接AP,CE.
如图,已知直线l1∥l2,线段AB在直线l1上,BC垂直于l1交l2于点C,且AB=BC,P是线段BC上异于两端点的一点,过点P的直线分别交l2,l1于点D,E(点A,E位于点B的两侧),满足BP=BE,连接AP,CE.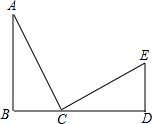 如图,已知:AB⊥BD,垂足为B,ED⊥BD,垂足为D,AB=CD,BC=DE,证明:AC⊥CE.
如图,已知:AB⊥BD,垂足为B,ED⊥BD,垂足为D,AB=CD,BC=DE,证明:AC⊥CE.