题目内容
15. 如图,抛物线y1=$\frac{1}{2}$(x+1)2+1与y2=a(x-4)2-3交于点A(1,3),过点A作x轴的平行线,分别交两条抛物线于B、C两点,且D、E分别为顶点.则下列结论:
如图,抛物线y1=$\frac{1}{2}$(x+1)2+1与y2=a(x-4)2-3交于点A(1,3),过点A作x轴的平行线,分别交两条抛物线于B、C两点,且D、E分别为顶点.则下列结论:①a=$\frac{2}{3}$;②AC=AE;③△ABD是等腰直角三角形;④当x>1时,y1>y2
其中正确结论的个数是( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 把点A坐标代入y2,求出a的值,即可得到函数解析式;令y=3,求出A、B、C的横坐标,然后求出BD、AD的长,利用勾股定理的逆定理以及结合二次函数图象分析得出答案.
解答 解:∵抛物线y1=$\frac{1}{2}$(x+1)2+1与y2=a(x-4)2-3交于点A(1,3),
∴3=a(1-4)2-3,
解得:a=$\frac{2}{3}$,故①正确;
过点E作EF⊥AC于点F,
∵E是抛物线的顶点,
∴AE=EC,E(4,-3),
∴AF=3,EF=6,
∴AE=$\sqrt{{6}^{2}+{3}^{2}}$=3$\sqrt{5}$,AC=2AF=6,
∴AC≠AE,故②错误;
当y=3时,3=$\frac{1}{2}$(x+1)2+1,
解得:x1=1,x2=-3,
故B(-3,3),D(-1,1),
则AB=4,AD=BD=2$\sqrt{2}$,
∴AD2+BD2=AB2,
∴③△ABD是等腰直角三角形,正确;
∵$\frac{1}{2}$(x+1)2+1=$\frac{2}{3}$(x-4)2-3时,
解得:x1=1,x2=37,
∴当37>x>1时,y1>y2,故④错误.
故选:B.
点评 本题考查了二次函数的性质,主要利用了待定系数法求二次函数解析式,已知函数值求自变量的值.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案
相关题目
5.为了迎接浙江省中小学生健康体质测试,某学校开展“健康校园,阳光跳绳”活动,为此学校准备购置A,B,C三种跳绳.已知某厂家的跳绳的规格与价格如下表:
(1)已知购买A,B两种绳子共20条花了180元,问A,B两种绳子各购买了多少条?
(2)若该厂家有一根长200米的绳子,现将其裁成A,C两种绳子销售总价为240元,则剩余的绳子长度最多可加工几条B种绳子?
(3)若该厂家有一根长200米的绳子,现将其裁成A,B,C三种绳子共40条(没有剩余)销售给学校,学校要求A种绳子的数量少于B种绳子的数量但不少于B种绳子的数量的一半,请直接写出所有的裁剪方案.
| A绳子 | B绳子 | C绳子 | |
| 长度(米) | 8 | 6 | 4 |
| 单价(元/条) | 12 | 8 | 6 |
(2)若该厂家有一根长200米的绳子,现将其裁成A,C两种绳子销售总价为240元,则剩余的绳子长度最多可加工几条B种绳子?
(3)若该厂家有一根长200米的绳子,现将其裁成A,B,C三种绳子共40条(没有剩余)销售给学校,学校要求A种绳子的数量少于B种绳子的数量但不少于B种绳子的数量的一半,请直接写出所有的裁剪方案.
10.如图,若用我们数学课本上采用的科学计算器进行计算,其按键顺序如下:

则输出结果应为( )

则输出结果应为( )
| A. | $\frac{1}{2}$ | B. | $\frac{13}{2}$ | C. | $\frac{17}{2}$ | D. | $\frac{25}{2}$ |
20.甲、乙两人用如图所示的两个转盘(每个转盘被分成面积相等的3个扇形)做游戏.游戏规则:转动两个转盘各一次,当转盘停止后,指针所在区域的数字之和为偶数时甲获胜;数字之和为奇数时乙获胜.若指针落在分界线上,则需要重新转动转盘.甲获胜的概率是( )


| A. | $\frac{1}{3}$ | B. | $\frac{4}{9}$ | C. | $\frac{5}{9}$ | D. | $\frac{2}{3}$ |
7.若代数式$\frac{\sqrt{x-2}}{\sqrt{x-1}}$有意义,则实数x的取值范围是( )
| A. | x≥1 | B. | x≥2 | C. | x>1 | D. | x>2 |
4. 如图,在⊙O中,AB是直径,CD是弦,AB⊥CD,垂足为E,连接CO,AD,∠BAD=20°,则下列说法中正确的是( )
如图,在⊙O中,AB是直径,CD是弦,AB⊥CD,垂足为E,连接CO,AD,∠BAD=20°,则下列说法中正确的是( )
 如图,在⊙O中,AB是直径,CD是弦,AB⊥CD,垂足为E,连接CO,AD,∠BAD=20°,则下列说法中正确的是( )
如图,在⊙O中,AB是直径,CD是弦,AB⊥CD,垂足为E,连接CO,AD,∠BAD=20°,则下列说法中正确的是( )| A. | AD=2OB | B. | CE=EO | C. | ∠OCE=40° | D. | ∠BOC=2∠BAD |
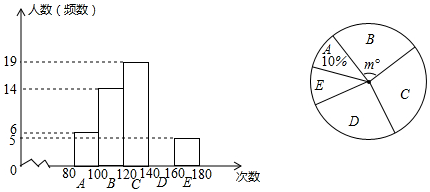
5. 为了传承中华优秀传统文化,市教育局决定开展“经典诵读进校园”活动,某校团委组织八年级100名学生进行“经典诵读”选拔赛,赛后对全体参赛学生的成绩进行整理,得到下列不完整的统计图表.
为了传承中华优秀传统文化,市教育局决定开展“经典诵读进校园”活动,某校团委组织八年级100名学生进行“经典诵读”选拔赛,赛后对全体参赛学生的成绩进行整理,得到下列不完整的统计图表.
请根据所给信息,解答以下问题:
(1)表中a=0.3,b=45;
(2)请计算扇形统计图中B组对应扇形的圆心角的度数;
(3)已知有四名同学均取得98分的最好成绩,其中包括来自同一班级的甲、乙两名同学,学校将从这四名同学中随机选出两名参加市级比赛,请用列表法或画树状图法求甲、乙两名同学都被选中的概率.
 为了传承中华优秀传统文化,市教育局决定开展“经典诵读进校园”活动,某校团委组织八年级100名学生进行“经典诵读”选拔赛,赛后对全体参赛学生的成绩进行整理,得到下列不完整的统计图表.
为了传承中华优秀传统文化,市教育局决定开展“经典诵读进校园”活动,某校团委组织八年级100名学生进行“经典诵读”选拔赛,赛后对全体参赛学生的成绩进行整理,得到下列不完整的统计图表.| 组别 | 分数段 | 频次 | 频率 |
| A | 60≤x<70 | 17 | 0.17 |
| B | 70≤x<80 | 30 | a |
| C | 80≤x<90 | b | 0.45 |
| D | 90≤x<100 | 8 | 0.08 |
(1)表中a=0.3,b=45;
(2)请计算扇形统计图中B组对应扇形的圆心角的度数;
(3)已知有四名同学均取得98分的最好成绩,其中包括来自同一班级的甲、乙两名同学,学校将从这四名同学中随机选出两名参加市级比赛,请用列表法或画树状图法求甲、乙两名同学都被选中的概率.