题目内容
 如图,在△ABC中,点D在BC上,AB=AC=CD,且AD=BD.求△ABC的三个内角.
如图,在△ABC中,点D在BC上,AB=AC=CD,且AD=BD.求△ABC的三个内角.考点:等腰三角形的性质
专题:
分析:设∠B=x,根据等边对等角表示出∠C,∠CAD=∠CDA,∠B=∠BAD,再根据三角形的一个外角等于与它不相邻的两个内角的和可得∠CDA=∠B+∠BAD,然后利用三角形的内角和定理列方程求出x,再求解即可.
解答:解:设∠B=x,
∵AB=AC,
∴∠C=x,
∵AC=CD,
∴∠CAD=∠CDA,
∵AD=BD,
∴∠B=∠BAD=x,
由三角形的外角性质得,∠CDA=∠B+∠BAD=2x,
在△ACD中,∠C+∠CAD+∠CDA=180°,
∴x+2x+2x=180°,
解得x=36°,
∴∠C=36°,
∠BAC=180°-36°-36°=108°,
所以,△ABC的三个内角分别是108°,36°,36°.
∵AB=AC,
∴∠C=x,
∵AC=CD,
∴∠CAD=∠CDA,
∵AD=BD,
∴∠B=∠BAD=x,
由三角形的外角性质得,∠CDA=∠B+∠BAD=2x,
在△ACD中,∠C+∠CAD+∠CDA=180°,
∴x+2x+2x=180°,
解得x=36°,
∴∠C=36°,
∠BAC=180°-36°-36°=108°,
所以,△ABC的三个内角分别是108°,36°,36°.
点评:本题考查了等腰三角形的性质,三角形的内角和定理,熟记性质并列出方程是解题的关键.

练习册系列答案
相关题目
下列各式中正确的是( )
A、
| ||
B、-
| ||
C、
| ||
D、±
|
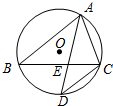 如图,⊙O是△ABC的外接圆,∠BAC的角平分线交BC于点E,交⊙O于点D,若AE=AC.求证:AB=AD.
如图,⊙O是△ABC的外接圆,∠BAC的角平分线交BC于点E,交⊙O于点D,若AE=AC.求证:AB=AD.