题目内容
关于函数y=3x2的性质的叙述，错误的是（ ）
| A、对称轴是y轴 |
| B、顶点是原点 |
| C、当x＞0时，y随x的增大而增大 |
| D、y有最大值 |
考点：二次函数的性质
专题：
分析：根据二次函数的性质得出函数y=3x2的对称轴及其增减性即可得出结论．
解答：解：∵函数y=3x2的顶点在原点，
∴其对称轴是y轴，顶点是原点，故A、B正确；
∵函数y=3x2的开口向上，顶点是原点，
∴当x＞0时，y随x的增大而增大，y有最小值，故C正确，D错误．
故选D．
∴其对称轴是y轴，顶点是原点，故A、B正确；
∵函数y=3x2的开口向上，顶点是原点，
∴当x＞0时，y随x的增大而增大，y有最小值，故C正确，D错误．
故选D．
点评：本题考查的是二次函数的性质，熟知二次函数y=ax2（a≠0）的顶点在原点，对称轴是y轴是解答此题的关键．
练习册系列答案
阳光课堂同步练习系列答案
相关题目
在如图所示的平面直角坐标系中，桥孔抛物线对应的二次函数关系式是y=-
如图，在直角坐标系中，△AOB是等边三角形，若B点的坐标是（2，0），则A点的坐标是对于函数y=3（x-2）2，下列说法正确的是（ ）
| A、当x＞0时，y随x的增大而减小 |
| B、当x＜0时，y随x的增大而增大 |
| C、当x＞2时，y随x的增大而增大 |
| D、当x＞-2时，y随x的增大而减小 |
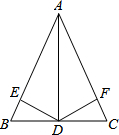如图，在△ABC中，AD是边BC的垂直平分线，DE⊥AB于E，DF⊥AC于F．