题目内容
 如图所示,正方形ABCD的边长是1,P为CD的中点,PQ⊥AP,交BC于Q,求BQ的长.
如图所示,正方形ABCD的边长是1,P为CD的中点,PQ⊥AP,交BC于Q,求BQ的长.考点:相似三角形的判定与性质,正方形的性质
专题:常规题型
分析:易证△ADP∽△PCQ,可得
=
,即可求BQ的值.
| AD |
| PC |
| DP |
| CQ |
解答:解:设BQ=x,则CQ=1-x,
在正方形ABCD中,∠C=∠D=90°,
∵∠APD+∠DAP=90°,
∠APD+∠CPQ=90°,
∴∠DAP=∠CPQ,
∴△ADP∽△PCQ,
∴
=
,
把AD=1,DP=PC=
代入上式,
解得x=
,即BQ=
.
在正方形ABCD中,∠C=∠D=90°,
∵∠APD+∠DAP=90°,
∠APD+∠CPQ=90°,
∴∠DAP=∠CPQ,
∴△ADP∽△PCQ,
∴
| AD |
| PC |
| DP |
| CQ |
把AD=1,DP=PC=
| 1 |
| 2 |
解得x=
| 3 |
| 4 |
| 3 |
| 4 |
点评:本题考查了相似三角形的判定,考查了相似三角形对应边比例相等的性质.

练习册系列答案
相关题目
下列图形中不是轴对称图形的是( )
A、 |
B、 |
C、 |
D、 |
下列关于x的方程中,一定是一元二次方程的为( )
| A、ax2+bx+c=0 |
| B、x2_2=(x+3)2 |
| C、2x+3x-5=0 |
| D、x2=-1 |
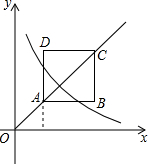 如图,正方形ABCD位于第一象限,AC=2
如图,正方形ABCD位于第一象限,AC=2| 2 |
| k |
| x |
| A、0<k≤1或k≥6 |
| B、1≤k≤6 |
| C、1≤k≤9 |
| D、0<k≤1或k≥9 |
已知Rt△ABC中,∠C=90°,BC=8,AB=10,则sinA=( )
A、
| ||
B、
| ||
C、
| ||
D、
|
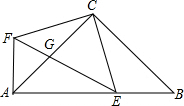 如图,在等腰Rt△ABC中,AC=BC,∠ACB=90°,点E在线段AB上,CF⊥CE,CF=CE,EF交AC于G,连接AF.
如图,在等腰Rt△ABC中,AC=BC,∠ACB=90°,点E在线段AB上,CF⊥CE,CF=CE,EF交AC于G,连接AF.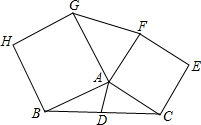 如图,已知AD是△ABC的中线,分别以AB、AC为边向外作正方形,得正方形ABHG和正方形ACEF,求证:
如图,已知AD是△ABC的中线,分别以AB、AC为边向外作正方形,得正方形ABHG和正方形ACEF,求证: 如图所示,AB=CD,BC=DA,∠ABC=∠BCD,求证:AB⊥AC.
如图所示,AB=CD,BC=DA,∠ABC=∠BCD,求证:AB⊥AC.