题目内容
 如图,正方形ABCD的边长为2,M为AD的中点,N在边CD上且∠NMB=∠MBC,MN的延长线与BC的延长线交于点G,则GN的长是
如图,正方形ABCD的边长为2,M为AD的中点,N在边CD上且∠NMB=∠MBC,MN的延长线与BC的延长线交于点G,则GN的长是考点:相似三角形的判定与性质,正方形的性质
专题:创新题型
分析:过M作MH⊥BC于H,得出四边形AMHB和四边形MDCH是矩形,先求证EF=BM,根据勾股定理求出BM、EF,求出△MBF面积,根据S△BHM+S△MHF=
得出
×1×2+
×(1+CF)×2=
,求出即可.
| 5 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 2 |
解答: 解:过M作MH⊥BC于H,
解:过M作MH⊥BC于H,
则四边形AMHB和四边形MDCH是矩形,
即DM=CH=1,BH=AM=1,MH=CD=2,
∵M为AD的中点,
∴AM=DM=
AD=
AB,
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠EBF=∠AMB,
∵EF⊥BM,
∴∠A=∠BEF=90°,
∴△EBF∽△AMB,
∴
=
=
,
∴EF=2BE=BM,
即BM=EF;
在Rt△ABM中,由勾股定理得:EF=BM=
=
,
S△BMF=
BM×EF=
×
×
=
,
∴S△BHM+S△MHF=
,
∴
×1×2+
×(1+CF)×2=
,
∴CF=
.
∵
=
,
∴CN=
,
∴根据勾股定理计算得FN=
2=
.
故答案为
.
 解:过M作MH⊥BC于H,
解:过M作MH⊥BC于H,则四边形AMHB和四边形MDCH是矩形,
即DM=CH=1,BH=AM=1,MH=CD=2,
∵M为AD的中点,
∴AM=DM=
| 1 |
| 2 |
| 1 |
| 2 |
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠EBF=∠AMB,
∵EF⊥BM,
∴∠A=∠BEF=90°,
∴△EBF∽△AMB,
∴
| EF |
| BE |
| AB |
| AM |
| 2 |
| 1 |
∴EF=2BE=BM,
即BM=EF;
在Rt△ABM中,由勾股定理得:EF=BM=
| 22+12 |
| 5 |
S△BMF=
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 5 |
| 5 |
| 2 |
∴S△BHM+S△MHF=
| 5 |
| 2 |
∴
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 2 |
∴CF=
| 1 |
| 2 |
∵
| CF |
| FH |
| CN |
| MH |
∴CN=
| 2 |
| 3 |
∴根据勾股定理计算得FN=
| CF2+CN |
| 5 |
| 6 |
故答案为
| 5 |
| 6 |
点评:本题考查了相似三角形的性质和判定,勾股定理,正方形性质等知识点,主要考查学生是否熟练运用性质进行推理和计算,题目综合性比较强,有一定的难度.

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案
相关题目
将圆周率π精确到千分位,应是( )
| A、3.14 |
| B、3.141 |
| C、3.1415 |
| D、3.142 |
下面生活中的实例,不是旋转的是( )
| A、螺旋桨的运动 |
| B、传送带传送货物 |
| C、风车风轮的运动 |
| D、自行车车轮的运动 |
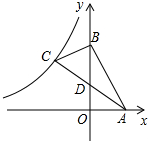 如图,直线y=-2x+6与坐标轴相交于点A、点B,BC⊥AB,且
如图,直线y=-2x+6与坐标轴相交于点A、点B,BC⊥AB,且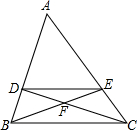 如图,已知DE∥BC,且BF:EF=4:3,则AE:EC=
如图,已知DE∥BC,且BF:EF=4:3,则AE:EC=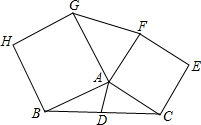 如图,已知AD是△ABC的中线,分别以AB、AC为边向外作正方形,得正方形ABHG和正方形ACEF,求证:
如图,已知AD是△ABC的中线,分别以AB、AC为边向外作正方形,得正方形ABHG和正方形ACEF,求证: