题目内容
甲、乙两人同解一个二元一次方程,甲抄错了常数项,得两根为3,2,乙抄错一次项系数得两根为-5和-1,求原来方程.
考点:根与系数的关系
专题:
分析:先设这个一元二次方程的两根是α、β,甲看错常数项,解得两根为3和2,说明3+2=-
,即α+β=5,乙看错一次项系数,解得两根为-5和-1,说明(-5)(-1)=
,即αβ=5,两式联合,可求关于以α、β为解的方程.
| b |
| a |
| c |
| a |
解答:解:甲看错常数项,解得两根为3和2,两根之和正确;乙看错一次项系数,解得两根为-5和-1,两根之积正确,
故设这个一元二次方程的两根是α、β,可得:α+β=5,αβ=5,
那么以α、β为两根的一元二次方程就是x2-5x+5=0.
故设这个一元二次方程的两根是α、β,可得:α+β=5,αβ=5,
那么以α、β为两根的一元二次方程就是x2-5x+5=0.
点评:此题主要考查了根与系数的关系,若x1、x2是方程ax2+bx+c=0的两根,则有x1+x2=-
,x1x2=
.
| b |
| a |
| c |
| a |

练习册系列答案
相关题目
 如图,直线y=2x-4交x轴、y轴于B、C,交双曲线y=
如图,直线y=2x-4交x轴、y轴于B、C,交双曲线y=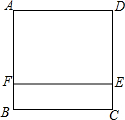 如图,从正方形ABCD上截取宽为2cm的矩形BCEF,剩下矩形AFED的面积为48cm2,则正方形ABCD的边长为
如图,从正方形ABCD上截取宽为2cm的矩形BCEF,剩下矩形AFED的面积为48cm2,则正方形ABCD的边长为 今年某区为绿化车道,用25600元购买甲、乙两种树苗共500棵,且这批树苗的成活率恰好为92%.有关甲、乙两种树苗的信息如图所示.
今年某区为绿化车道,用25600元购买甲、乙两种树苗共500棵,且这批树苗的成活率恰好为92%.有关甲、乙两种树苗的信息如图所示.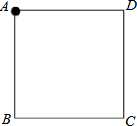 一枚棋子依次沿正方形ABCD的四个顶点A、B、C、D、A、B、C、D…移动,开始时棋子在A点(如图),然后根据骰子所掷点数移动棋子(如掷了1点,则移动1格到B,如掷6点,则移动6格到C等),移动后到达的点为新的出发点,再次进行同样的游戏.
一枚棋子依次沿正方形ABCD的四个顶点A、B、C、D、A、B、C、D…移动,开始时棋子在A点(如图),然后根据骰子所掷点数移动棋子(如掷了1点,则移动1格到B,如掷6点,则移动6格到C等),移动后到达的点为新的出发点,再次进行同样的游戏.