题目内容
 如图,直线y=2x-4交x轴、y轴于B、C,交双曲线y=
如图,直线y=2x-4交x轴、y轴于B、C,交双曲线y=| k |
| x |
考点:反比例函数与一次函数的交点问题
专题:
分析:首先作辅助线:过点E作ED⊥x轴于D,可得△COB∽△EDB,根据相似三角形的对应边成比例,即可得
=
=
=
,从而求得E的坐标,然后把E的坐标代入双曲线的解析式即可求得k的值.
| OC |
| ED |
| OB |
| BD |
| BC |
| BE |
| 2 |
| 1 |
解答: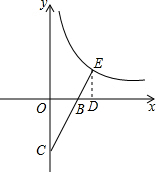 解:过点E作ED⊥x轴于D,
解:过点E作ED⊥x轴于D,
∵直线y=2x-4,
∴B(2,0),C(0,-4),
∴OB=2,OC=4
∵OC∥ED,
∴△COB∽△EDB,
∴
=
=
=
,
∴ED=2,BD=1,
∴OD=3,
∴E(3,2)
∵点E在双曲线y=
上,
∴2=
,
解得k=6.
 解:过点E作ED⊥x轴于D,
解:过点E作ED⊥x轴于D,∵直线y=2x-4,
∴B(2,0),C(0,-4),
∴OB=2,OC=4
∵OC∥ED,
∴△COB∽△EDB,
∴
| OC |
| ED |
| OB |
| BD |
| BC |
| BE |
| 2 |
| 1 |
∴ED=2,BD=1,
∴OD=3,
∴E(3,2)
∵点E在双曲线y=
| k |
| x |
∴2=
| k |
| 3 |
解得k=6.
点评:此题考查了反比例函数的性质,相似三角形的判定与性质.此题综合性较强,注意数形结合思想的应用.

练习册系列答案
相关题目
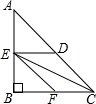 如图,在Rt△ABC中,∠ABC=90°,过AB的中点E分别作BC和AC的平行线,交AC于点D,交BC于点F,连接CE.你能发现得到的四个小三角形有什么关系,为什么?
如图,在Rt△ABC中,∠ABC=90°,过AB的中点E分别作BC和AC的平行线,交AC于点D,交BC于点F,连接CE.你能发现得到的四个小三角形有什么关系,为什么?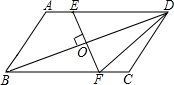 已知:如图,AD∥BC,O为BD的中点,EF⊥BD于点O,与AD,BC分别交于点E,F.下列结论正确的是( )
已知:如图,AD∥BC,O为BD的中点,EF⊥BD于点O,与AD,BC分别交于点E,F.下列结论正确的是( )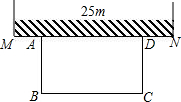 如图,某农场老板准备建造一个矩形羊圈ABCD,他打算让矩形羊圈的一面完全靠着墙MN,墙MN可利用的长度为25m,另外三面用长度为50m的篱笆围成(篱笆正好要全部用完,且不考虑接头的部分)
如图,某农场老板准备建造一个矩形羊圈ABCD,他打算让矩形羊圈的一面完全靠着墙MN,墙MN可利用的长度为25m,另外三面用长度为50m的篱笆围成(篱笆正好要全部用完,且不考虑接头的部分) 如图,一艘海上巡逻船在A巡航,这时接到B海上指挥中心紧急通知:在指挥中心北偏西60°方向的C有一艘渔船遇险,要求马上前去救援.此时C位于A北偏西30°方向上,A位于B北偏西75°方向上.AB之间的距离为12.求A、C两地之间的距离.(参考数据:
如图,一艘海上巡逻船在A巡航,这时接到B海上指挥中心紧急通知:在指挥中心北偏西60°方向的C有一艘渔船遇险,要求马上前去救援.此时C位于A北偏西30°方向上,A位于B北偏西75°方向上.AB之间的距离为12.求A、C两地之间的距离.(参考数据: