题目内容
14.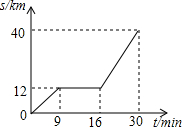 如图所示为某汽车行驶的路程S(km)与时间t(min)的函数关系图,观察图中所提供的信息解答下列问题:
如图所示为某汽车行驶的路程S(km)与时间t(min)的函数关系图,观察图中所提供的信息解答下列问题:(1)汽车在前9分钟内的平均速度是多少?
(2)汽车中途停了多长时间?
(3)当16≤t≤30时,求S与t的函数关系式?
分析 (1)根据速度=路程÷时间,列式计算即可得解;
(2)根据停车时路程没有变化列式计算即可;
(3)利用待定系数法求一次函数解析式解答即可.
解答 解:(1)平均速度=$\frac{12}{9}$=$\frac{4}{3}$km/min;
(2)从9分到16分,路程没有变化,停车时间t=16-9=7min.
(3)设函数关系式为S=kt+b,
将(16,12),C(30,40)代入得,
$\left\{\begin{array}{l}{16k+b=12}\\{30k+b=40}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=2}\\{b=-20}\end{array}\right.$.
所以,当16≤t≤30时,求S与t的函数关系式为S=2t-20.
点评 本题考查了一次函数的应用,待定系数法求函数解析式,比较简单,准确识图并获取信息是解题的关键.

练习册系列答案
相关题目
2. 如图,平行四边形ABCD的周长为16cm,AC,BD相交于点O,EO⊥BD交AD于点E,则△ABE的周长为( )
如图,平行四边形ABCD的周长为16cm,AC,BD相交于点O,EO⊥BD交AD于点E,则△ABE的周长为( )
 如图,平行四边形ABCD的周长为16cm,AC,BD相交于点O,EO⊥BD交AD于点E,则△ABE的周长为( )
如图,平行四边形ABCD的周长为16cm,AC,BD相交于点O,EO⊥BD交AD于点E,则△ABE的周长为( )| A. | 4cm | B. | 6cm | C. | 8cm | D. | 10cm |
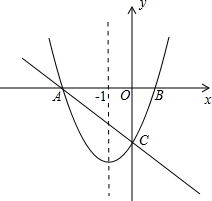 如图,在直角坐标系xOy中,一次函数y=-$\frac{2}{3}$x+m(m为常数)的图象与x轴交于A(-3,0),与y轴交于点C.以直线x=-1为对称轴的抛物线y=ax+bx+c(a,b,c为常数,且a>0)经过A、C两点,与x轴正半轴交于点B.
如图,在直角坐标系xOy中,一次函数y=-$\frac{2}{3}$x+m(m为常数)的图象与x轴交于A(-3,0),与y轴交于点C.以直线x=-1为对称轴的抛物线y=ax+bx+c(a,b,c为常数,且a>0)经过A、C两点,与x轴正半轴交于点B.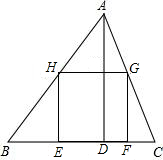 如图,△ABC是一张锐角三角形余料,其中BC=12cm,高AD=6cm,现在要把它剪成一个正方形材料备用,使正方形的一边在BC上,其余两个顶点分别在AB,AC上,则这个正方形材料的边长是多少?
如图,△ABC是一张锐角三角形余料,其中BC=12cm,高AD=6cm,现在要把它剪成一个正方形材料备用,使正方形的一边在BC上,其余两个顶点分别在AB,AC上,则这个正方形材料的边长是多少? 如图,直线y=-$\frac{4}{3}$x+4与x轴、y轴分别交于点A,B,点C是线段AB上一点,四边形OADC是菱形,则OD的长=4.8.
如图,直线y=-$\frac{4}{3}$x+4与x轴、y轴分别交于点A,B,点C是线段AB上一点,四边形OADC是菱形,则OD的长=4.8. 如图,路灯(P)距地面8米,身高1.6米的佳佳从点A沿OA所在直线行走10米到点D时,身影变短了2.5米.
如图,路灯(P)距地面8米,身高1.6米的佳佳从点A沿OA所在直线行走10米到点D时,身影变短了2.5米. 如图,已知等边△ABC.
如图,已知等边△ABC.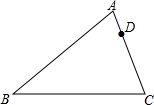 如图,已知在△ABC中,AB=14,BC=12,AC=10,D是AC上一点,且AD=4,过点D画一条直线l,把△ABC分成两部分,使其中的一个三角形与△ABC相似,请在图中画出所有符合要求的直线l,并写出所作三角形与△ABC的相似比.
如图,已知在△ABC中,AB=14,BC=12,AC=10,D是AC上一点,且AD=4,过点D画一条直线l,把△ABC分成两部分,使其中的一个三角形与△ABC相似,请在图中画出所有符合要求的直线l,并写出所作三角形与△ABC的相似比.