题目内容
3. 如图,已知等边△ABC.
如图,已知等边△ABC.(1)请用圆规和直尺作△ABC的内切圆(要求保留作图痕迹,不必写作法和证明);
(2)若等边△ABC边长为2,求△ABC的内切圆的半径.
分析 (1)分别作∠ABC和∠ACB的平分线,它们相交于点O,其中∠ABC的平分线交AC于D,然后以O点为圆心,OD为半径作圆即可;
(2)根据等边三角形的性质得BD⊥AC,AD=CD=$\frac{1}{2}$AC=1而∠OCD=$\frac{1}{2}$∠ACB=30°,则在Rt△OCD中可利用∠OCD的正切计算出OD,从而得到△ABC的内切圆的半径.
解答 解:(1)如图,⊙O为所求;
(2)∵△ABC为等边三角形,
而BD平分∠ABC,
∴BD⊥AC,AD=CD=$\frac{1}{2}$AC=1,
∵OC平分∠ACB,
∴∠OCD=$\frac{1}{2}$∠ACB=30°,
在Rt△OCD中,∵tan∠OCD=$\frac{OD}{CD}$,
∴OD=1×tan30°=$\frac{\sqrt{3}}{3}$,
即△ABC的内切圆的半径为$\frac{\sqrt{3}}{3}$.
点评 本题考查了作图-复杂作图:复杂作图是在五种基本作图的基础上进行作图,一般是结合了几何图形的性质和基本作图方法.解决此类题目的关键是熟悉基本几何图形的性质,结合几何图形的基本性质把复杂作图拆解成基本作图,逐步操作.也考查了三角形的内切圆与内心.

练习册系列答案
相关题目
13.已知m<0,那么|$\sqrt{{m}^{2}}$-2m|值为( )
| A. | m | B. | -m | C. | 3m | D. | -3m |
12. 如图,数轴上表示的是一个不等式的解集,则这个不等式组可能是( )
如图,数轴上表示的是一个不等式的解集,则这个不等式组可能是( )
 如图,数轴上表示的是一个不等式的解集,则这个不等式组可能是( )
如图,数轴上表示的是一个不等式的解集,则这个不等式组可能是( )| A. | $\left\{\begin{array}{l}{y≥-1}\\{x<2}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x≤-1}\\{x>2}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x<-1}\\{x≥2}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x>-1}\\{x≤2}\end{array}\right.$ |
13. 如图,已知直线a∥b,∠1=40°,∠2=100°,则∠3等于( )
如图,已知直线a∥b,∠1=40°,∠2=100°,则∠3等于( )
 如图,已知直线a∥b,∠1=40°,∠2=100°,则∠3等于( )
如图,已知直线a∥b,∠1=40°,∠2=100°,则∠3等于( )| A. | 40° | B. | 60° | C. | 80° | D. | 100° |
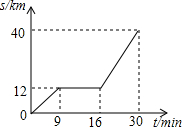 如图所示为某汽车行驶的路程S(km)与时间t(min)的函数关系图,观察图中所提供的信息解答下列问题:
如图所示为某汽车行驶的路程S(km)与时间t(min)的函数关系图,观察图中所提供的信息解答下列问题: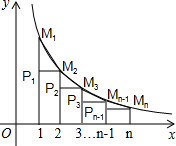 如图,已知反比例函数y=$\frac{1}{x}$的图象,当x取1,2,3,…n时,对应在反比例图象上的点分别为M1、M2、M3…Mn,则S△P1M1M2+S△P2M2M3+…S△Pn-1Mn-1Mn=$\frac{n-1}{2n}$.
如图,已知反比例函数y=$\frac{1}{x}$的图象,当x取1,2,3,…n时,对应在反比例图象上的点分别为M1、M2、M3…Mn,则S△P1M1M2+S△P2M2M3+…S△Pn-1Mn-1Mn=$\frac{n-1}{2n}$. 如图,在△ABC中,AB=AC,D是AB的中点,且DE⊥AB.已知△BCE的周长为12,且AC-BC=2,求AB,BC的长.
如图,在△ABC中,AB=AC,D是AB的中点,且DE⊥AB.已知△BCE的周长为12,且AC-BC=2,求AB,BC的长.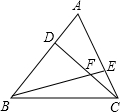 已知D,E分别是△ABC的边AB,AC上的点,且AD=$\frac{1}{3}$AB,CE=$\frac{1}{3}$AC,EB,CD交于点F,则S△FBC:S△ABC=$\frac{2}{7}$.
已知D,E分别是△ABC的边AB,AC上的点,且AD=$\frac{1}{3}$AB,CE=$\frac{1}{3}$AC,EB,CD交于点F,则S△FBC:S△ABC=$\frac{2}{7}$.