题目内容
10. 如图,方格纸中的每个小方格都是边长为1个单位的正方形,Rt△ABC的顶点均在格点上,建立平面直角坐标系后,点A的坐标为(-4,1),点C的坐标为(-1,1),将Rt△ABC按一定的规律变换:第一次,将Rt△ABC沿AC边翻折,得Rt△AB1C;第二次,将Rt△AB1C绕点B1逆时针旋转90°,得Rt△A1B1C1;第三次,将Rt△A1B1C1沿A1C1边翻折,得Rt△A1B2C1;第四次,将Rt△A1B2C1绕点B2逆时针90°,得Rt△A2B2C2…如此依次下去
如图,方格纸中的每个小方格都是边长为1个单位的正方形,Rt△ABC的顶点均在格点上,建立平面直角坐标系后,点A的坐标为(-4,1),点C的坐标为(-1,1),将Rt△ABC按一定的规律变换:第一次,将Rt△ABC沿AC边翻折,得Rt△AB1C;第二次,将Rt△AB1C绕点B1逆时针旋转90°,得Rt△A1B1C1;第三次,将Rt△A1B1C1沿A1C1边翻折,得Rt△A1B2C1;第四次,将Rt△A1B2C1绕点B2逆时针90°,得Rt△A2B2C2…如此依次下去(1)试在图中画出Rt△A1B1C1和Rt△A2B2C2,并写出A1的坐标(-3,-4);
(2)请直接写出在第11次变换后所得的点B的对应的点的坐标是(-5,-1).
分析 (1)利用网格特点和对称轴变换和旋转的性质画出Rt△A1B1C1和Rt△A2B2C2,从而得到A1的坐标;
(2)通过画图可得到第8次变换后所得△A4B4C4与△ABC重合,即没8次变换一个循环,于是可判断第11次变换与第3次变换的图形一样,然后写出B2的坐标即可.
解答 解:(1)如图,Rt△A1B1C1和Rt△A2B2C2为所作,A1的坐标为(-3,-4);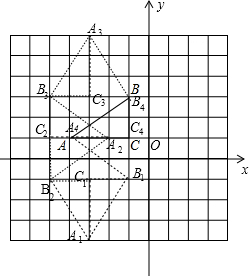
(2)第8次变换后所得△A4B4C4与△ABC重合,
所以第11次变换后的三角形与△A1B2C1重合,
所以所得的点B的对应的点的坐标为(-5,-1).
故答案为(-3,-4),(-5,-1).
点评 本题考查了作图-旋转变换:根据旋转的性质可知,对应角都相等都等于旋转角,对应线段也相等,由此可以通过作相等的角,在角的边上截取相等的线段的方法,找到对应点,顺次连接得出旋转后的图形.也考查了轴对称变换.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.下列命题中,是真命题的是( )
| A. | 对角线互相垂直的平行四边形是正方形 | |
| B. | 相似三角形的周长之比等于相似的平方 | |
| C. | 若(1,y1)、(2,y2)是双曲线y=-$\frac{1}{x}$上的两点,则y1<y2 | |
| D. | 方程x2-2x+3=0有两个不相等的实数根 |
5. 有理数a、b在数轴上对应的点分别为A、B(如图所示),则有理数a、b、-a的大小关系为( )
有理数a、b在数轴上对应的点分别为A、B(如图所示),则有理数a、b、-a的大小关系为( )
 有理数a、b在数轴上对应的点分别为A、B(如图所示),则有理数a、b、-a的大小关系为( )
有理数a、b在数轴上对应的点分别为A、B(如图所示),则有理数a、b、-a的大小关系为( )| A. | -a<a<b | B. | b<-a<a | C. | a<-a<b | D. | a<b<-a |
15. 如图,A、D是电线杆AB上的两个瓷壶,AC和DE分别表示太阳光线,若某一时刻线段AD在地面上的影长CE=1m,BD在地面上的影长BE=3m,瓷壶D到地面的距离DB=20m,则电线杆AB的高为( )
如图,A、D是电线杆AB上的两个瓷壶,AC和DE分别表示太阳光线,若某一时刻线段AD在地面上的影长CE=1m,BD在地面上的影长BE=3m,瓷壶D到地面的距离DB=20m,则电线杆AB的高为( )
 如图,A、D是电线杆AB上的两个瓷壶,AC和DE分别表示太阳光线,若某一时刻线段AD在地面上的影长CE=1m,BD在地面上的影长BE=3m,瓷壶D到地面的距离DB=20m,则电线杆AB的高为( )
如图,A、D是电线杆AB上的两个瓷壶,AC和DE分别表示太阳光线,若某一时刻线段AD在地面上的影长CE=1m,BD在地面上的影长BE=3m,瓷壶D到地面的距离DB=20m,则电线杆AB的高为( )| A. | 15m | B. | $\frac{80}{3}$m | C. | 21m | D. | $\frac{60}{7}$m |
 如图,在直线y=-x+4与x轴交于A点,与y轴交于B点,抛物线y=-x2+bx+c经过A、B两点.
如图,在直线y=-x+4与x轴交于A点,与y轴交于B点,抛物线y=-x2+bx+c经过A、B两点. 如图,某测量员测量公园内一棵树DE的高度,他们在这棵树左侧一斜坡上端点A处测得树顶端D的仰角为30°,朝着这棵树的方向走到台阶下的点C处,测得树顶端D的仰角为60°.已知A点的高度AB为3米,台阶AC的坡度为1:$\sqrt{3}$(即AB:BC=1:$\sqrt{3}$),且B、C、E三点在同一条直线上.
如图,某测量员测量公园内一棵树DE的高度,他们在这棵树左侧一斜坡上端点A处测得树顶端D的仰角为30°,朝着这棵树的方向走到台阶下的点C处,测得树顶端D的仰角为60°.已知A点的高度AB为3米,台阶AC的坡度为1:$\sqrt{3}$(即AB:BC=1:$\sqrt{3}$),且B、C、E三点在同一条直线上.