题目内容
19. 如图,在?ABCD中,点E在BC边上,且AE⊥BC于点E,ED平分∠CDA,若BE:EC=1:2,则∠BCD的度数为120°.
如图,在?ABCD中,点E在BC边上,且AE⊥BC于点E,ED平分∠CDA,若BE:EC=1:2,则∠BCD的度数为120°.
分析 由平行四边形的性质和已知条件得出∠CED=∠CDE,证出CD=EC=AB,得出BE=$\frac{1}{2}$AB,再在Rt△ABE中求出∠BAE,得出∠B,即可求出∠BCD的度数.
解答 解:∵四边形ABCD是平行四边形,
∴AB=CD,AD∥BC,AB∥CD,
∴∠ADE=∠CED,∠B+∠BCD=180°,
∵ED平分∠CDA,
∴∠ADE=∠CDE,
∴∠CED=∠CDE,
∴CD=EC,
∴AB=EC,
∵BE:EC=1:2,
∴BE:AB=1:2,
即BE=$\frac{1}{2}$AB,
∵AE⊥BC,
∴∠AEB=90°,
∴∠BAE=30°,
∴∠B=60°,
∴∠BCD=120°;
故答案为:120°.
点评 本题考查了平行四边形的性质、等腰三角形的判定、三角函数;熟练掌握平行四边形的性质,并能进行推理计算是解决问题的关键.

练习册系列答案
相关题目
9.下列运算正确的是( )
| A. | a2•a3=a5 | B. | (x2)3=x5 | C. | m6÷m2=m3 | D. | 6a-4a=2 |
14.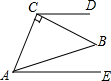 如图,CD∥AE,∠ACB=90°,AC=BC,∠BCD=20°,则∠EAB的度数为( )
如图,CD∥AE,∠ACB=90°,AC=BC,∠BCD=20°,则∠EAB的度数为( )
 如图,CD∥AE,∠ACB=90°,AC=BC,∠BCD=20°,则∠EAB的度数为( )
如图,CD∥AE,∠ACB=90°,AC=BC,∠BCD=20°,则∠EAB的度数为( )| A. | 15° | B. | 20° | C. | 25° | D. | 30° |
4.把m3-9m分解因式正确的是( )
| A. | m(m2-9) | B. | m(m-3)2 | C. | m(m+3)(m-3) | D. | m(m+9)(m-9) |
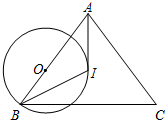 如图,在△ABC中,I是内心,O是AB边上一点,⊙O经过B点且与AI相切于I点.
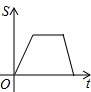
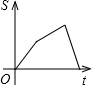
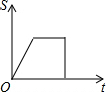
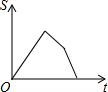
如图,在△ABC中,I是内心,O是AB边上一点,⊙O经过B点且与AI相切于I点. 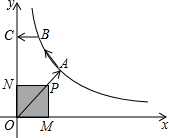 如图,已知A、B是反比例函数y=$\frac{k}{x}$(k>0,x>0)图象上的两点,BC∥x轴,交y轴于点C,动点P纵坐标原点O出发,沿O→A→B→C匀速运动,终点为C,过点P作PM⊥x轴,PN⊥y轴,垂足分别为M、N.设四边形OMPN的面积为S,点P运动的时间为t,则S关于t的函数图象大致为( )
如图,已知A、B是反比例函数y=$\frac{k}{x}$(k>0,x>0)图象上的两点,BC∥x轴,交y轴于点C,动点P纵坐标原点O出发,沿O→A→B→C匀速运动,终点为C,过点P作PM⊥x轴,PN⊥y轴,垂足分别为M、N.设四边形OMPN的面积为S,点P运动的时间为t,则S关于t的函数图象大致为( )