题目内容
8.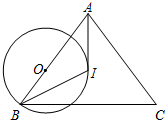 如图,在△ABC中,I是内心,O是AB边上一点,⊙O经过B点且与AI相切于I点.
如图,在△ABC中,I是内心,O是AB边上一点,⊙O经过B点且与AI相切于I点. (1)求证:AB=AC;
(2)若BC=16,⊙O的半径是5,求AI的长.
分析 (1)延长AI交BC于D,连结OI,作BH⊥AC于H,如图,根据内心的性质得∠OBI=∠DBI,则可证明OI∥BD,再根据切线的性质得OI⊥AI,则BD⊥AD,加上AI平分∠BAC,所以△ABC为等腰三角形,得到AB=AC;
(2)由OI∥BC,得到△AOI∽△ABD,得到比例式,再根据勾股定理求得AD=$\sqrt{AB2-BD2}$=$\frac{32}{3}$,于是就可得.
解答 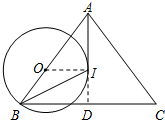 解:(1)延长AI交BC于D,连结OI,作BH⊥AC于H,如图,
解:(1)延长AI交BC于D,连结OI,作BH⊥AC于H,如图,
∵I是△ABC的内心,
∴BI平分∠ABC,即∠OBI=∠DBI,
∵OB=OI,
∴∠OBI=∠OIB,
∴∠DBI=∠OIB,
∴OI∥BD,
∵AI为⊙O的切线,
∴OI⊥AI,
∴BD⊥AD,
∵AI平分∠BAC,
∴△ABC为等腰三角形,
∴AB=AC;
(2)∵OI∥BC,
∴△AOI∽△ABD,
∴$\frac{AO}{AB}$=$\frac{OI}{BD}$=$\frac{AI}{AD}$,
∴$\frac{AB-5}{AB}$=$\frac{5}{8}$,
∴AB=$\frac{40}{3}$,
∴AD=$\sqrt{AB2-BD2}$=$\frac{32}{3}$,
∴AI=$\frac{OI}{BD}$•AD=$\frac{5}{8}$×$\frac{32}{3}$=$\frac{20}{3}$.
点评 本题考查了三角形的内切圆与内心,等腰三角形的判定和性质,相似三角形的判定和性质,勾股定理,正确的作出辅助线是解题的关键.

练习册系列答案
相关题目
16.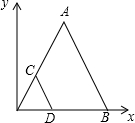 如图,把△COD扩大后得到△AOB,若点C,D,B的坐标分别为C(1,2),D(2,0),B(5,0).则点A的坐标为( )
如图,把△COD扩大后得到△AOB,若点C,D,B的坐标分别为C(1,2),D(2,0),B(5,0).则点A的坐标为( )
 如图,把△COD扩大后得到△AOB,若点C,D,B的坐标分别为C(1,2),D(2,0),B(5,0).则点A的坐标为( )
如图,把△COD扩大后得到△AOB,若点C,D,B的坐标分别为C(1,2),D(2,0),B(5,0).则点A的坐标为( )| A. | (2,5) | B. | (2.5,5) | C. | (2,5) | D. | (3,6) |
17.为了了解某班学生每天使用零花钱数(单位:元)的情况,小王随机调查了15名同学,结果如下表:
则这15名同学每天使用零花钱的众数和中位数分别是( )
| 每天使用零花钱数 | 1 | 2 | 3 | 5 | 6 |
| 人数 | 2 | 5 | 4 | 3 | 1 |
| A. | 2元、3元 | B. | 2.5元、3元 | C. | 2元、2.5元 | D. | 3元、2.5元 |
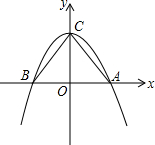 如图,抛物线y=-$\frac{1}{2}$x2+2与x轴交于A、B两点,其中点A在x轴的正半轴上,点B在x轴的负半轴上
如图,抛物线y=-$\frac{1}{2}$x2+2与x轴交于A、B两点,其中点A在x轴的正半轴上,点B在x轴的负半轴上 如图,在?ABCD中,点E在BC边上,且AE⊥BC于点E,ED平分∠CDA,若BE:EC=1:2,则∠BCD的度数为120°.
如图,在?ABCD中,点E在BC边上,且AE⊥BC于点E,ED平分∠CDA,若BE:EC=1:2,则∠BCD的度数为120°.
 如图,线段AC与BD相交于点O,连接AB,CD,若AB∥CD,BO=DO,AF=CE.
如图,线段AC与BD相交于点O,连接AB,CD,若AB∥CD,BO=DO,AF=CE.