��Ŀ����
11�����������ĸ����⣺�ٽ�һ��n���ε�ֽƬ�ü�����ȥһ���ǣ�n��4�Ҽ�������ֱ�ߣ�����ʣ�µ�ֽƬ��n-1��n+1�ߣ�����x-|x-3|=1����x=1��3������֪����y=��2k-3��xk-3$+\frac{2}{x}$�ǹ���x�ķ�������������k=$\frac{3}{2}$������֪���κ���y=ax2+bx+c��a��0��a-b+c��0����b2-4ac��0��������ȷ�������У�������| A�� | 0�� | B�� | 1�� | C�� | 2�� | D�� | 3�� |
���� ���÷������۶Ԣٽ����жϣ����ݸ�����ָ���ݵ�����Ԣڽ����жϣ����ݷ����������Ķ���Ԣ۽����жϣ����ݶ��κ���ͼ����ϵ���Ĺ�ϵ�õ���������x�����������㣬��ɶԢܽ����жϣ�
��� �⣺��һ��n���ε�ֽƬ�ü�����ȥһ���ǣ�n��4�Ҽ�������ֱ�ߣ�����ʣ�µ�ֽƬ��n-1��n��n+1�ߣ����Ԣٴ���
��x-|x-3|=1����x=1��-1��3�����Ԣڴ���
��֪����y=��2k-3��xk-3$+\frac{2}{x}$�ǹ���x�ķ�������������k=$\frac{3}{2}$��k=2�����Ԣ۴���
��֪���κ���y=ax2+bx+c��a��0��a-b+c��0����b2-4ac��0�����Ԣܴ���
��ѡA��
���� ���⿼���������붨�����ж�һ���������䣬�������⣮�������ⶼ��������ͽ�����������ɣ���������֪�������������֪�����Ƴ������һ���������д�ɡ��������ô������ʽ����Щ�������ȷ����������֤ʵ�ģ����������������������

��ϰ��ϵ�д�
�����Ŀ
16��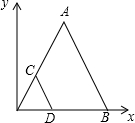 ��ͼ���ѡ�COD�����õ���AOB������C��D��B������ֱ�ΪC��1��2����D��2��0����B��5��0�������A������Ϊ��������
��ͼ���ѡ�COD�����õ���AOB������C��D��B������ֱ�ΪC��1��2����D��2��0����B��5��0�������A������Ϊ��������
 ��ͼ���ѡ�COD�����õ���AOB������C��D��B������ֱ�ΪC��1��2����D��2��0����B��5��0�������A������Ϊ��������
��ͼ���ѡ�COD�����õ���AOB������C��D��B������ֱ�ΪC��1��2����D��2��0����B��5��0�������A������Ϊ��������| A�� | ��2��5�� | B�� | ��2.5��5�� | C�� | ��2��5�� | D�� | ��3��6�� |
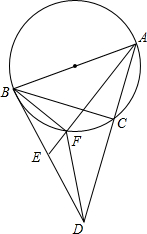 ��ͼ����֪�ڡ�ABC�У�AB��BC������B����ABC�����Բ�����ߣ���AC���ӳ����ڵ�D��EΪBD���е㣬����AE����ABC�����Բ�ڵ�F����֤����CBF=��BDF��
��ͼ����֪�ڡ�ABC�У�AB��BC������B����ABC�����Բ�����ߣ���AC���ӳ����ڵ�D��EΪBD���е㣬����AE����ABC�����Բ�ڵ�F����֤����CBF=��BDF��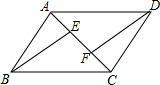 ��֪���ı���ABCD�У�AB=CD��BC=AD��E��F�ֱ��ǶԽ���AC�����㣬��AE=CF��
��֪���ı���ABCD�У�AB=CD��BC=AD��E��F�ֱ��ǶԽ���AC�����㣬��AE=CF�� ��ͼ����?ABCD�У���E��BC���ϣ���AE��BC�ڵ�E��EDƽ�֡�CDA����BE��EC=1��2�����BCD�Ķ���Ϊ120�㣮
��ͼ����?ABCD�У���E��BC���ϣ���AE��BC�ڵ�E��EDƽ�֡�CDA����BE��EC=1��2�����BCD�Ķ���Ϊ120�㣮