题目内容
 如图,CD切⊙O于P,PE⊥AB于E,AC⊥CD,BD⊥CD,求证:
如图,CD切⊙O于P,PE⊥AB于E,AC⊥CD,BD⊥CD,求证:(1)PE:AC=PB:PA.
(2)PE2=AC•BD.
考点:切线的性质,相似三角形的判定与性质
专题:证明题
分析:(1)根据弦切角定理得到∠CPA=∠PBA,则根据三角形相似的判定方法易得Rt△PBE∽Rt△APC,于是利用相似的性质有PE:AC=PB:PA;
(2)利用比例性质由PE:AC=PB:PA得PE=
•AC①,同样可证明Rt△PAE∽RtBPD,也得到PE=
•BD②,然后把①、②两式相乘即可得到结论.
(2)利用比例性质由PE:AC=PB:PA得PE=
| PB |
| PA |
| PA |
| PB |
解答:证明:(1)∵CD切⊙O于P,
∴∠CPA=∠PBA,
∵PE⊥AB,AC⊥CD,
∴∠PEB=90°,∠ACP=90°,
∴Rt△PBE∽Rt△APC,
∴PE:AC=PB:PA;
(2)∵PE:AC=PB:PA
∴PE=
•AC①,
同理可证明Rt△PAE∽RtBPD,
∴PE:BD=AP:PB,
∴PE=
•BD②,
由①②得PE2=
•AC•
•BD=AC•BD.
∴∠CPA=∠PBA,
∵PE⊥AB,AC⊥CD,
∴∠PEB=90°,∠ACP=90°,
∴Rt△PBE∽Rt△APC,
∴PE:AC=PB:PA;
(2)∵PE:AC=PB:PA
∴PE=
| PB |
| PA |
同理可证明Rt△PAE∽RtBPD,
∴PE:BD=AP:PB,
∴PE=
| PA |
| PB |
由①②得PE2=
| PB |
| PA |
| PA |
| PB |
点评:本题考查了切线的性质:圆的切线垂直于经过切点的半径.也考查了弦切角定理和相似三角形的判定与性质.

练习册系列答案
相关题目
 如图,△ABC的顶点A、B、C均在⊙O上,AB=AC,∠AOC=60°,则∠ACB的大小是( )
如图,△ABC的顶点A、B、C均在⊙O上,AB=AC,∠AOC=60°,则∠ACB的大小是( )| A、30° | B、45° |
| C、60° | D、70° |
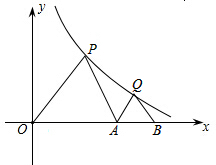 △POA、△QAB都是等边三角形,点P、Q都在双曲线y=
△POA、△QAB都是等边三角形,点P、Q都在双曲线y=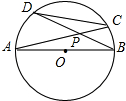 如图,⊙O的直径AB=10,CD是⊙O的弦,AC与BD相交于点P.
如图,⊙O的直径AB=10,CD是⊙O的弦,AC与BD相交于点P.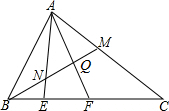 如图,在△ABC中,M是AC的中点,E、F是BC上的两点,且BE=EF=FC,求BN:NQ:QM的值.
如图,在△ABC中,M是AC的中点,E、F是BC上的两点,且BE=EF=FC,求BN:NQ:QM的值.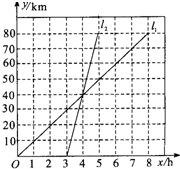 如图表示小王骑自行车和小李骑摩托车都沿相同的路线由甲地到乙地行驶过程的函数图象,两地相距80千米,请根据图象解决下列问题:
如图表示小王骑自行车和小李骑摩托车都沿相同的路线由甲地到乙地行驶过程的函数图象,两地相距80千米,请根据图象解决下列问题: 探索规律:观察如图由“※”组成的图案和算式,解答问题:
探索规律:观察如图由“※”组成的图案和算式,解答问题: