题目内容
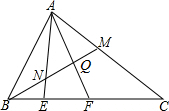 如图,在△ABC中,M是AC的中点,E、F是BC上的两点,且BE=EF=FC,求BN:NQ:QM的值.
如图,在△ABC中,M是AC的中点,E、F是BC上的两点,且BE=EF=FC,求BN:NQ:QM的值.考点:平行线分线段成比例
专题:计算题
分析:连结MF,如图,先证明MF为△CEA的中位线,则AE=2MF,AE∥MF,利用NE∥MF得到
=
=1,
=
=
,即BN=NM,MF=2NF,设BN=a,NE=b,则NM=a,MF=2b,AE=4b,所以AN=3b,然后利用AN∥MF得到
=
=
=
,所以NQ=
a,QM=
a,再计算BN:NQ:QM的值.
| BN |
| NM |
| BE |
| EF |
| NE |
| MF |
| BE |
| BF |
| 1 |
| 2 |
| NQ |
| QM |
| AN |
| MF |
| 3b |
| 2b |
| 3 |
| 2 |
| 3 |
| 5 |
| 2 |
| 5 |
解答:解:连结MF,如图,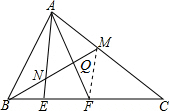
∵M是AC的中点,EF=FC,
∴MF为△CEA的中位线,
∴AE=2MF,AE∥MF,
∵NE∥MF,
∴
=
=1,
=
=
,
∴BN=NM,MF=2NF,
设BN=a,NE=b,则NM=a,MF=2b,AE=4b,
∴AN=3b,
∵AN∥MF,
∴
=
=
=
,
∴NQ=
a,QM=
a,
∴BN:NQ:QM=a:
a:
a=5:3:2.

∵M是AC的中点,EF=FC,
∴MF为△CEA的中位线,
∴AE=2MF,AE∥MF,
∵NE∥MF,
∴
| BN |
| NM |
| BE |
| EF |
| NE |
| MF |
| BE |
| BF |
| 1 |
| 2 |
∴BN=NM,MF=2NF,
设BN=a,NE=b,则NM=a,MF=2b,AE=4b,
∴AN=3b,
∵AN∥MF,
∴
| NQ |
| QM |
| AN |
| MF |
| 3b |
| 2b |
| 3 |
| 2 |
∴NQ=
| 3 |
| 5 |
| 2 |
| 5 |
∴BN:NQ:QM=a:
| 3 |
| 5 |
| 2 |
| 5 |
点评:本题考查了平行线分线段成比例:三条平行线截两条直线,所得的对应线段成比例.也考查了三角形中位线性质.

练习册系列答案
相关题目
已知某商店铺第17届仁川亚运会吉祥物毛绒玩具每件的进价为30元,在某段时间内若以每件x元(30≤x≤50,且x为整数)出售,可卖出(50-x)件,若要使该店铺销售该玩具的利润最大,每件的售价为( )
| A、35元 | B、40元 |
| C、45元 | D、48元 |
下列结论错误的个数是( )
①若a>0,b>0,则a+b>0;
②若a<0,b<0,则a+b<0;
③若a>0,b>0,则a+b>0.
①若a>0,b>0,则a+b>0;
②若a<0,b<0,则a+b<0;
③若a>0,b>0,则a+b>0.
| A、0个 | B、1个 | C、2个 | D、3个 |
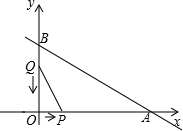 如图,在平面直角坐标系中,OA=12cm,OB=6cm,点P从点O开始沿OA向点A移动,点Q从点B开始沿BO向点O移动,点P、Q的移动速度都是1cm/s,如果点P、Q同时出发,用t(s)表示移动的时间(0≤t≤6),那么
如图,在平面直角坐标系中,OA=12cm,OB=6cm,点P从点O开始沿OA向点A移动,点Q从点B开始沿BO向点O移动,点P、Q的移动速度都是1cm/s,如果点P、Q同时出发,用t(s)表示移动的时间(0≤t≤6),那么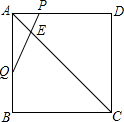 如图,正方形ABCD中,点P为边AD上一点,DP=3AP,点Q为边AB的中点,连接PQ交对角线AC于点E.试求
如图,正方形ABCD中,点P为边AD上一点,DP=3AP,点Q为边AB的中点,连接PQ交对角线AC于点E.试求 如图,CD切⊙O于P,PE⊥AB于E,AC⊥CD,BD⊥CD,求证:
如图,CD切⊙O于P,PE⊥AB于E,AC⊥CD,BD⊥CD,求证: