题目内容
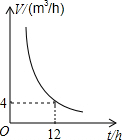 如图是某一蓄水池的排水速度V(m3/h)与排完水池中的水所用的时间t(h)之间的函数关系图象.
如图是某一蓄水池的排水速度V(m3/h)与排完水池中的水所用的时间t(h)之间的函数关系图象.(1)直接写出此函数的解析式和自变量t的取值范围;
(2)如果要6h排完水池中的水,那么每小时的排水量应该是多少?
(3)如果每小时排水量是5m3,那么水池中的水要用多少小时排完?
考点:反比例函数的应用
专题:
分析:(1)此题根据点(12,4)在此函数图象上,利用待定系数法求出函数的解析式,结合实际意义求出自变量t的取值范围;
(2)此题须把t=6代入函数的解析式即可求出每小时的排水量;
(3)由V=5,列出方程,求方程即可.
(2)此题须把t=6代入函数的解析式即可求出每小时的排水量;
(3)由V=5,列出方程,求方程即可.
解答:解:(1)设此函数的解析式为V=
,
∵点(12,4)在此函数图象上,
∴4=
,解得k=48,
∴此函数的解析式V=
,
∵t表示排水所用的时间,
∴t>0;
(2)当t=6时,V=
=8m3;
故如果要6h排完水池中的水,那么每小时的排水量应该是8m3;
(3)∵V=5,
∴
=5,
∴t=9.6.
故水池中的水要用9.6小时排完.
| k |
| t |
∵点(12,4)在此函数图象上,
∴4=
| k |
| 12 |
∴此函数的解析式V=
| 48 |
| t |
∵t表示排水所用的时间,
∴t>0;
(2)当t=6时,V=
| 48 |
| 6 |
故如果要6h排完水池中的水,那么每小时的排水量应该是8m3;
(3)∵V=5,
∴
| 48 |
| t |
∴t=9.6.
故水池中的水要用9.6小时排完.
点评:主要考查了反比例函数的应用.解题的关键是根据实际意义列出函数关系式,从实际意义中找到对应的变量的值,利用待定系数法求出函数解析式.会用方程解决实际问题.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目
 已知如图,一次函数y=kx+b的图象与反比例函数y=
已知如图,一次函数y=kx+b的图象与反比例函数y=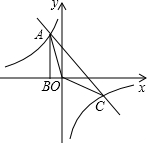 如图,Rt△ABO的顶点A是双曲线
如图,Rt△ABO的顶点A是双曲线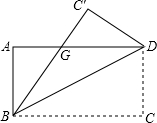 如图,一张矩形纸片ABCD,其中AD=8cm,AB=6cm,先沿对角线BD对折,点C落在点C′的位置,BC′交AD于点G.
如图,一张矩形纸片ABCD,其中AD=8cm,AB=6cm,先沿对角线BD对折,点C落在点C′的位置,BC′交AD于点G.