题目内容
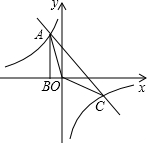 如图,Rt△ABO的顶点A是双曲线y=
如图,Rt△ABO的顶点A是双曲线y=| k |
| x |
| 5 |
| 2 |
(1)求这两个函数的解析式.
(2)若直线与双曲线的两个交点为A、C,求△AOC的面积.
(3)根据图象,直接写出使一次函数的值小于反比例函数的值的x的取值范围.
考点:反比例函数与一次函数的交点问题
专题:
分析:(1)根据三角形面积即可求出k,代入即可;
(2)解由两函数组成的方程组,求出A、C的坐标,求出D的坐标,根据三角形面积公式求出即可;
(3)根据图象和A、C的坐标即可得出答案.
(2)解由两函数组成的方程组,求出A、C的坐标,求出D的坐标,根据三角形面积公式求出即可;
(3)根据图象和A、C的坐标即可得出答案.
解答:解:(1)设A的坐标是(x,y),
则OB=-x,AB=y,
∵S△ABO=
,
∴
×OB×AB=
,
∴OB×AB=5,
∴xy=-5,
即k=-5,
∴直线的解析式是y=-x+4,反比例函数的解析式是y=-
;
(2)解方程组
得:
,
,
即A的坐标是(-1,5),C的坐标是(5,-1),
设直线y=-x+4和y轴的交点为D,如图,
把x=0代入y=-x+4得:y=4,
即OD=4,
S△AOC=S△AOD+S△COD=
×4×1+
×4×5=12;
(3)使一次函数的值小于反比例函数的值的x的取值范围是-1<x<0或x>5.
则OB=-x,AB=y,
∵S△ABO=
| 5 |
| 2 |
∴
| 1 |
| 2 |
| 5 |
| 2 |
∴OB×AB=5,
∴xy=-5,
即k=-5,
∴直线的解析式是y=-x+4,反比例函数的解析式是y=-
| 5 |
| x |
(2)解方程组
|
|
|
即A的坐标是(-1,5),C的坐标是(5,-1),
设直线y=-x+4和y轴的交点为D,如图,
把x=0代入y=-x+4得:y=4,
即OD=4,
S△AOC=S△AOD+S△COD=
| 1 |
| 2 |
| 1 |
| 2 |
(3)使一次函数的值小于反比例函数的值的x的取值范围是-1<x<0或x>5.
点评:本题考查了一次函数和反比例函数的交点问题,用待定系数法求函数的解析式,三角形的面积的应用,主要考查学生的计算能力,题目比较好,难度适中.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 A、B、C、D、E 5个车站的位置如图,分别求出D、E两站和A、E两站的距离(单位:km).
A、B、C、D、E 5个车站的位置如图,分别求出D、E两站和A、E两站的距离(单位:km). 如图是某一蓄水池的排水速度V(m3/h)与排完水池中的水所用的时间t(h)之间的函数关系图象.
如图是某一蓄水池的排水速度V(m3/h)与排完水池中的水所用的时间t(h)之间的函数关系图象.