题目内容
 已知如图,一次函数y=kx+b的图象与反比例函数y=
已知如图,一次函数y=kx+b的图象与反比例函数y=| n |
| x |
(1)求上述反比例函数和一次函数的表达式;
(2)求△AOB的面积.
考点:反比例函数与一次函数的交点问题
专题:
分析:(1)把A的坐标代入反比例函数的解析式,即可求出反比例函数的解析式,求出B的坐标,把A、B的坐标代入一次函数的解析式,得出方程组,求出方程组的解,即可得出一次函数的解析式;
(2)求出C的坐标,根据三角形的面积公式求出三角形AOC和三角形BOC的面积,即可得出答案.
(2)求出C的坐标,根据三角形的面积公式求出三角形AOC和三角形BOC的面积,即可得出答案.
解答:解:(1)∵点A(-3,1)在反比例函数y=
的图象上,
∴n=(-3)×1=-3,
∴反比例函数的表达式为y=-
,
∵点B(1,m)也在反比例函数的y=-
图象上,
∴m=-3,即B(1,-3),
把点A(-3,1),点B(1,-3)代入一次函数y=kx+b中,得
,
解得:
,
∴一次函数的表达式为y=-x-2;
(2)如图,在y=-x-2中,当y=0时,得x=-2,
∴直线y=-x-2与x轴的交点为C(-2,0),
∵线段OC将△AOB分成△AOC和△BOC,
∴S△AOB=S△AOC+S△BOC=
×2×3+
×2×1=3+1=4.
| n |
| x |
∴n=(-3)×1=-3,
∴反比例函数的表达式为y=-
| 3 |
| x |
∵点B(1,m)也在反比例函数的y=-
| 3 |
| x |
∴m=-3,即B(1,-3),
把点A(-3,1),点B(1,-3)代入一次函数y=kx+b中,得
|
解得:
|
∴一次函数的表达式为y=-x-2;
(2)如图,在y=-x-2中,当y=0时,得x=-2,
∴直线y=-x-2与x轴的交点为C(-2,0),
∵线段OC将△AOB分成△AOC和△BOC,
∴S△AOB=S△AOC+S△BOC=
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查了三角形的面积,用待定系数法求函数的图象,一次函数和反比例函数的交点问题的应用,主要考查学生的计算能力,题目比较好,难度适中.

练习册系列答案
相关题目
在梯形ABCD中,AD∥BC,那么∠A:∠B:∠C:∠D可能为( )
| A、3:4:5:2 |
| B、2:3:4:5 |
| C、5:3:4:2 |
| D、5:4:3:2 |
 A、B、C、D、E 5个车站的位置如图,分别求出D、E两站和A、E两站的距离(单位:km).
A、B、C、D、E 5个车站的位置如图,分别求出D、E两站和A、E两站的距离(单位:km).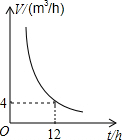 如图是某一蓄水池的排水速度V(m3/h)与排完水池中的水所用的时间t(h)之间的函数关系图象.
如图是某一蓄水池的排水速度V(m3/h)与排完水池中的水所用的时间t(h)之间的函数关系图象.