题目内容
20.(1)x2+4x-140=0.(2)x2-6x+6=0.
(3)2x2=6x-1.
分析 (1)运用因式分解法进行解答;
(2)运用公式法进行解答;
(3)把原方程化为一般形式,运用公式法进行解答.
解答 解:(1)x2+4x-140=0,
(x+14)(x-10)=0,
x1=-14,x2=10;
(2)x=$\frac{6±\sqrt{12}}{2}$=3±$\sqrt{3}$,
x1=3+$\sqrt{3}$,x2=3-$\sqrt{3}$;
(3)原方程可化为2x2-6x+1=0,
x=$\frac{6±\sqrt{28}}{4}$=$\frac{3±\sqrt{7}}{2}$,
x1=$\frac{3+\sqrt{7}}{2}$,x2=$\frac{3-\sqrt{7}}{2}$.
点评 本题考查的是一元二次方程的解法,灵活运用配方法、公式法、因式分解法解方程是解题的关键.

练习册系列答案
相关题目
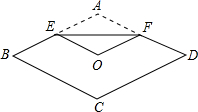 如图,将菱形纸片ABCD折叠,使点A恰好落在菱形的对称中心O处,折痕为EF.若EF=2,则此菱形纸片ABCD对角线BD的长为4.
如图,将菱形纸片ABCD折叠,使点A恰好落在菱形的对称中心O处,折痕为EF.若EF=2,则此菱形纸片ABCD对角线BD的长为4.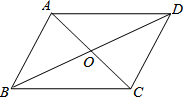 如图,?ABCD的周长是28cm,△ABC的周长是22cm,对角线交于点O,则OC的长为4cm.
如图,?ABCD的周长是28cm,△ABC的周长是22cm,对角线交于点O,则OC的长为4cm.