题目内容
8．已知正六边形边长为2，则它的内切圆面积为3π．分析 根据题意画出图形，利用正六边形中的等边三角形的性质求得内切圆半径，再根据圆的面积公式求解即可．
解答 
解：如图，连接OA、OB，OG；
∵六边形ABCDEF是边长为4的正六边形，
∴△OAB是等边三角形，
∴OA=AB=2，
∴OG=OA•sin60°=2×$\frac{\sqrt{3}}{2}$=$\sqrt{3}$，
∴边长为2的正六边形的内切圆的半径为$\sqrt{3}$，
∴内切圆面积为π×（$\sqrt{3}$）2=3π．
故答案为：3π．
点评 考查了正多边形和圆，本题涉及到正多边形、等边三角形及特殊角的三角函数值，难度适中．
练习册系列答案
相关题目
，则
的值为( )
16．下列计算中，正确的是（ ）
| A． | 2$\sqrt{3}$-$\sqrt{3}$=2 | B． | 2+$\sqrt{2}$=2$\sqrt{2}$ | C． | $\sqrt{8}$-$\sqrt{2}$=$\sqrt{2}$ | D． | $\sqrt{9}$-$\sqrt{4}$=$\sqrt{5}$ |
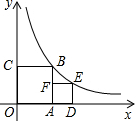如图，正方形OABC，ADEF的顶点A，D，C在坐标轴上，点F在AB上，点B，E在函数y=$\frac{1}{x}$（x＞0）的图象上，则：