题目内容
15．当k＜9 时，方程x2-6x+k=0有两个不相等的实数根．分析 根据△＞0列出不等式求解即可．
解答 解：∵方程x2-6x+k=0有两个不相等的实数根，
∴△=b2-4ac=（-6）2-4×1×k＞0，
解得k＜9．
故答案为：k＜9．
点评 本题考查了一元二次方程ax2+bx+c=0（a≠0，a，b，c为常数）的根的判别式△=b2-4ac．当△＞0，方程有两个不相等的实数根；当△=0，方程有两个相等的实数根；当△＜0，方程没有实数根．
练习册系列答案
阅读快车系列答案
相关题目
的两个解是
和
、
的值；
的代数式表示
；
是不小于
的负数，求
的取值范围．
6．计算（-2）100+（-2）99的结果是（ ）
| A． | 2 | B． | -2 | C． | -299 | D． | 299 |
10．一元二次方程（x-2）2=0的解为（ ）
| A． | x1=2，x2=-2 | B． | x1=x2=2 | C． | x=-2 | D． | x1=2，x2=0 |
4．
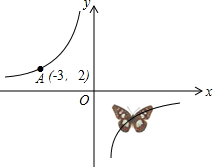如图，反比例函数y=$\frac{k}{x}$（k≠0，k是常数）的图象经过A点，则该函数图象上被蝴蝶遮住的点的坐标可能是（ ）
如图，反比例函数y=$\frac{k}{x}$（k≠0，k是常数）的图象经过A点，则该函数图象上被蝴蝶遮住的点的坐标可能是（ ）| A． | （-2，3） | B． | （2，-2） | C． | （-1，6） | D． | （2，-3） |
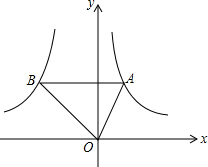如图，点A是反比例函数y1=$\frac{2}{x}$（x＞0）图象上的任意一点，过点A作 AB∥x轴，交另一个比例函数y2=$\frac{k}{x}$（k＜0，x＜0）的图象于点B．