题目内容
9.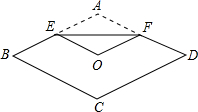 如图,将菱形纸片ABCD折叠,使点A恰好落在菱形的对称中心O处,折痕为EF.若EF=2,则此菱形纸片ABCD对角线BD的长为4.
如图,将菱形纸片ABCD折叠,使点A恰好落在菱形的对称中心O处,折痕为EF.若EF=2,则此菱形纸片ABCD对角线BD的长为4.
分析 根据菱形的性质得出AC⊥BD,根据折叠得出EF⊥AC,EF平分AO,得出EF∥BD,得出EF为△ABD的中位线,根据三角形中位线定理求出即可.
解答 解:如图所示:连接BD、AC.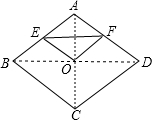 ∵四边形ABCD是菱形,
∵四边形ABCD是菱形,
∴AC⊥BD,
∵A沿EF折叠与O重合,
∴EF⊥AC,EF平分AO,
∵AC⊥BD,
∴EF∥BD,
∴E、F分别为AB、AD的中点,
∴EF为△ABD的中位线,
∴EF=$\frac{1}{2}$BD,
∴BD=2EF=4;
故答案为:4.
点评 本题考查了折叠的性质、菱形的性质、三角形中位线定理;熟练掌握菱形的性质和翻折变换的性质,并能进行推理论证与计算是解决问题的关键.

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
4.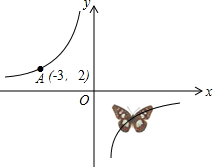 如图,反比例函数y=$\frac{k}{x}$(k≠0,k是常数)的图象经过A点,则该函数图象上被蝴蝶遮住的点的坐标可能是( )
如图,反比例函数y=$\frac{k}{x}$(k≠0,k是常数)的图象经过A点,则该函数图象上被蝴蝶遮住的点的坐标可能是( )
 如图,反比例函数y=$\frac{k}{x}$(k≠0,k是常数)的图象经过A点,则该函数图象上被蝴蝶遮住的点的坐标可能是( )
如图,反比例函数y=$\frac{k}{x}$(k≠0,k是常数)的图象经过A点,则该函数图象上被蝴蝶遮住的点的坐标可能是( )| A. | (-2,3) | B. | (2,-2) | C. | (-1,6) | D. | (2,-3) |
14.若a>b,则下列结论正确的是( )
| A. | a-5<b-5 | B. | a+2<b+2 | C. | 3a<3b | D. | -3a<-3b |
16.若分式方程$\frac{x+1}{x-2}$=$\frac{k}{x-2}$无解,则k( )
| A. | k=-1 | B. | k=1 | C. | k=3 | D. | k=0 |
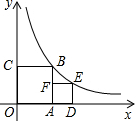 如图,正方形OABC,ADEF的顶点A,D,C在坐标轴上,点F在AB上,点B,E在函数y=$\frac{1}{x}$(x>0)的图象上,则:
如图,正方形OABC,ADEF的顶点A,D,C在坐标轴上,点F在AB上,点B,E在函数y=$\frac{1}{x}$(x>0)的图象上,则: 如图,AE是△ABC的角平分线,ED平分∠AEB且垂直AB
如图,AE是△ABC的角平分线,ED平分∠AEB且垂直AB