题目内容
8.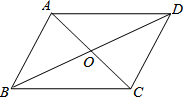 如图,?ABCD的周长是28cm,△ABC的周长是22cm,对角线交于点O,则OC的长为4cm.
如图,?ABCD的周长是28cm,△ABC的周长是22cm,对角线交于点O,则OC的长为4cm.
分析 由平行四边形的性质得出AB=CD,AD=BC,OA=OC=$\frac{1}{2}$AC,由已知条件得出AB+BC=14cm,由△ABC的周长得出AC的长,即可得出OC的长.
解答 解:∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC,OA=OC=$\frac{1}{2}$AC,
∵?ABCD的周长是28cm,
∴AB+BC=14cm,
∵△ABC的周长是22cm,
∴AB+BC+AC=22cm,
∴AC=22cm-14cm=8cm,
∴OC=$\frac{1}{2}$AC=4cm.
故答案为:4.
点评 本题考查了平行四边形的性质、三角形和平行四边形的周长;熟练掌握平行四边形的性质,并能进行推理计算是解决问题的关键.

练习册系列答案
相关题目
16.若分式方程$\frac{x+1}{x-2}$=$\frac{k}{x-2}$无解,则k( )
| A. | k=-1 | B. | k=1 | C. | k=3 | D. | k=0 |
17.等腰三角形的一个内角是50°,则这个等腰三角形底角的度数是( )
| A. | 80° | B. | 50° | C. | 50°或80° | D. | 65°或50° |
 如图,AE是△ABC的角平分线,ED平分∠AEB且垂直AB
如图,AE是△ABC的角平分线,ED平分∠AEB且垂直AB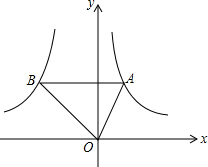 如图,点A是反比例函数y1=$\frac{2}{x}$(x>0)图象上的任意一点,过点A作 AB∥x轴,交另一个比例函数y2=$\frac{k}{x}$(k<0,x<0)的图象于点B.
如图,点A是反比例函数y1=$\frac{2}{x}$(x>0)图象上的任意一点,过点A作 AB∥x轴,交另一个比例函数y2=$\frac{k}{x}$(k<0,x<0)的图象于点B.