题目内容
11.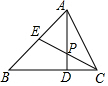 如图,△ABC中,AD⊥BC于点D,CE平分∠ACB交AD于点P,交AB于点E,若∠ABC=45°,∠APE=55°,则∠BAC的度数是65°.
如图,△ABC中,AD⊥BC于点D,CE平分∠ACB交AD于点P,交AB于点E,若∠ABC=45°,∠APE=55°,则∠BAC的度数是65°.
分析 在△CDP中利用三角形内角和定理即可得出∠DCP的度数,由角平分线的定义即可得出∠ACB的度数,再在△ABC中利用三角形内角和定理即可求出∠BAC的度数.
解答 解:∵AD⊥BC,∠CPD=∠APE=55°,
∴∠CDP=90°,
∴∠DCP=180°-∠CPD-∠CDP=35°.
∵CE平分∠ACB,
∴∠ACB=2∠DCP=70°,
∴∠BAC=180°-∠ABC-∠ACB=180°-45°-70°=65°.
故答案为:65°.
点评 本题考查了三角形内角和定理、角平分线的定义、垂直以及对顶角,利用三角形内角和定理结合角平分线的定义找出∠ACB的度数是解题的关键.

练习册系列答案
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案
相关题目
3.某圆形零件的制作成本y(元)与它的面积成正比例,设半径为r(cm),当r=2cm时,y=20元,那么当制作成本为125元时,半径是( )
| A. | 5cm | B. | $\frac{25}{π}$cm | C. | 10cm | D. | 25cm |
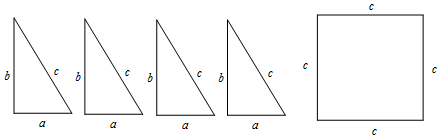
1.某超市货架上摆放着桶装方便面,如图是它们的三视图,则货架上的桶装方便面至少有( )


| A. | 8桶 | B. | 9桶 | C. | 10桶 | D. | 11桶 |
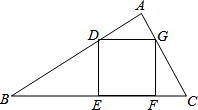 在△ABC中,正方形DEFG的两个顶点E、F在BC边上,另两个顶点D、G分别在AB、AC上,△ADG和△CFG的面积均为1,△BDE的面积为3,求正方形DEFG的面积.
在△ABC中,正方形DEFG的两个顶点E、F在BC边上,另两个顶点D、G分别在AB、AC上,△ADG和△CFG的面积均为1,△BDE的面积为3,求正方形DEFG的面积. 已知实数a,b,c在数轴上的位置如图,求式子|c-b|-|-b|+$\sqrt{{a}^{2}}$+|a+c|的值.
已知实数a,b,c在数轴上的位置如图,求式子|c-b|-|-b|+$\sqrt{{a}^{2}}$+|a+c|的值. 已知直线y=-2x+4与x轴、y轴分别交于A、D两点,抛物线y=ax2-x+c经过点A、D,点B是抛物线与x轴的另一个交点.
已知直线y=-2x+4与x轴、y轴分别交于A、D两点,抛物线y=ax2-x+c经过点A、D,点B是抛物线与x轴的另一个交点.