题目内容
19.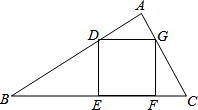 在△ABC中,正方形DEFG的两个顶点E、F在BC边上,另两个顶点D、G分别在AB、AC上,△ADG和△CFG的面积均为1,△BDE的面积为3,求正方形DEFG的面积.
在△ABC中,正方形DEFG的两个顶点E、F在BC边上,另两个顶点D、G分别在AB、AC上,△ADG和△CFG的面积均为1,△BDE的面积为3,求正方形DEFG的面积.
分析 过A作AM⊥BC于M,交DG于N,设正方形DEFG的边长是a,AN=b,根据三角形面积公式求出BE=3b,CF=b,ab=2,推出b=$\frac{2}{a}$①,根据S正方形DEFG=S△ABC-(S△ADG+S△BDE+S△CFG)求出a=2b②,由①②即可求出答案.
解答 解:过A作AM⊥BC于M,交DG于N,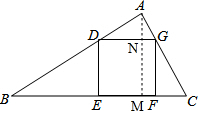
设正方形DEFG的边长是a,AN=b,
∵四边形DEFG是正方形,
∴DG=GF=EF=DE=MN=a,DG∥BC,
∵S△ADG=1,S△BDE=3,S△FCG=1,
∴$\frac{1}{2}$ab=1,$\frac{1}{2}$BE•a=3,$\frac{1}{2}$CF•a=1,
∴BE=3b,CF=b,
∴S△ADG+S△BED+SCFG=$\frac{1}{2}$ab+$\frac{1}{2}$ab+$\frac{1}{2}$ab=1+3+1=5,
∴ab=2,
∴b=$\frac{2}{a}$①,
∵S正方形DEFG=S△ABC-(S△ADG+S△BDE+S△CFG)
=$\frac{1}{2}$(BE+EF+CF)×(AN+MN)-(S△ADG+S△BDE+S△CFG)
=$\frac{1}{2}$(a+4b)(a+b)-5=a2,
∴a=2b②,
由①②得:a=2,
即正方形的边长是2,
∴正方形DEFG的面积=4.
点评 本题考查了相似三角形的性质和判定,三角形面积公式,正方形的性质的应用,注意:相似三角形的面积比等于相似比的平方.

练习册系列答案
相关题目
4.把m、n同时扩大2倍,分式值保持不变的分式是( )
| A. | $\frac{m+1}{n}$ | B. | $\frac{m+1}{n+1}$ | C. | $\frac{m}{n+m}$ | D. | $\frac{m-n}{n-1}$ |
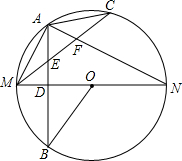 如图所示,MN是⊙O的直径,作AB⊥MN,垂足为点D,连接AM,AN,点C为弧AN上一点,且$\widehat{AC}$=$\widehat{AM}$,连接CM,交AB于点E,交AN于点F,现给出以下结论:①MD=DO;②$\widehat{AM}$=$\widehat{BM}$;③∠ACM+∠ANM=∠MOB;④AE=$\frac{1}{2}$MF.其中正确的结论有②③④.(请把所有正确结论的序号都填在横线上)
如图所示,MN是⊙O的直径,作AB⊥MN,垂足为点D,连接AM,AN,点C为弧AN上一点,且$\widehat{AC}$=$\widehat{AM}$,连接CM,交AB于点E,交AN于点F,现给出以下结论:①MD=DO;②$\widehat{AM}$=$\widehat{BM}$;③∠ACM+∠ANM=∠MOB;④AE=$\frac{1}{2}$MF.其中正确的结论有②③④.(请把所有正确结论的序号都填在横线上)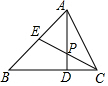 如图,△ABC中,AD⊥BC于点D,CE平分∠ACB交AD于点P,交AB于点E,若∠ABC=45°,∠APE=55°,则∠BAC的度数是65°.
如图,△ABC中,AD⊥BC于点D,CE平分∠ACB交AD于点P,交AB于点E,若∠ABC=45°,∠APE=55°,则∠BAC的度数是65°.