题目内容
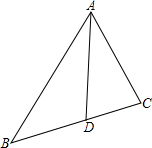 如图,△ABC的角平分线AD交BC于点D,
如图,△ABC的角平分线AD交BC于点D,(1)若AB=10,AC=6,求:
| S△ABD |
| S△ACD |
(2)若AB=a,AC=b,∠BAD=∠DAC=α,求证:S△ABC=ab•sinαcosα,
并用a,b和角α的三角函数表示角平分线AD的长.(注:不能使用课本未出现的结论)
考点:解直角三角形
专题:
分析:(1)求出
=
=
,再根据三角形的面积公式求出即可;
(2)求出sin2α=2sinαcosα,解子三角形求出CW,根据三角形的面积公式求出即可;过D作DT⊥AB于T,DZ⊥AC于Z,根据角平分线的性质得出DT=DZ,设DT=DZ=e,根据三角形的面积公式得出S△ABC=S△ADB+S△ADC,求出DT=e=
,在Rt△ATD中解直角三角形即可.
| AB |
| AC |
| BD |
| CD |
| 5 |
| 3 |
(2)求出sin2α=2sinαcosα,解子三角形求出CW,根据三角形的面积公式求出即可;过D作DT⊥AB于T,DZ⊥AC于Z,根据角平分线的性质得出DT=DZ,设DT=DZ=e,根据三角形的面积公式得出S△ABC=S△ADB+S△ADC,求出DT=e=
| 2absinαcosα |
| a+b |
解答:解:(1)
=
,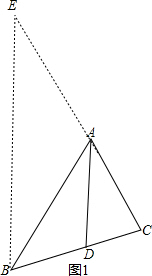
理由是:如图1,过B作BE∥AD,交CA的延长线于E,
∵AD是角平分线,
∴∠CAD=∠DAB,
∵AD∥BE,
∴∠CAD=∠E,∠DAB=∠ABE,
∴∠E=∠ABE,
∴AE=AB,
∵AD∥BE,
∴
=
,
∴
=
=
=
,
∴
=
=
,
∴
=
=
=
;
证明:(2)如图2,设在△DEF中,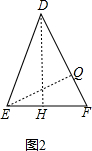
∠EDF=2α,DE=DF=x,EF=2y,
过D作DH⊥EF于H,则EH=FH=y,∠EDH=∠FDH=α,
由勾股定理得:DH=
,
sinα=
=
,cosα=
=
,
所以sinαcosα=
,
∵由三角形面积公式得:
EF×DH=
DF×EQ,
∴EQ=
=
,
∴sin2a=
=
,
∴sin2α=2sinαcosα,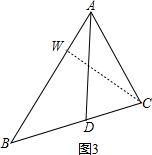
如图3,过C作CW⊥AB于W,
则CW=AC×sin2α=bsin2α,
∴S△ABC=
AB×CW=
×absin2α,
∵sin2α=2sinαcosα,
∴S△ABC=absinαcosα.
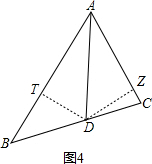
如图4,过D作DT⊥AB于T,DZ⊥AC于Z,
∵AD是角平分线,
∴DT=DZ,
设DT=DZ=e,
根据三角形的面积公式得:S△ABC=S△ADB+S△ADC,
absinαcosα=
ae+
be,
∴DT=e=
,
在Rt△ATD中,AD=
=
=
.
| S△ABD |
| S△ACD |
| 5 |
| 3 |

理由是:如图1,过B作BE∥AD,交CA的延长线于E,
∵AD是角平分线,
∴∠CAD=∠DAB,
∵AD∥BE,
∴∠CAD=∠E,∠DAB=∠ABE,
∴∠E=∠ABE,
∴AE=AB,
∵AD∥BE,
∴
| AC |
| AE |
| CD |
| BD |
∴
| AC |
| AB |
| CD |
| BD |
| 6 |
| 10 |
| 3 |
| 5 |
∴
| AB |
| AC |
| BD |
| DC |
| 5 |
| 3 |
∴
| S△ABD |
| S△ACD |
| BD |
| CD |
| AB |
| AC |
| 5 |
| 3 |
证明:(2)如图2,设在△DEF中,

∠EDF=2α,DE=DF=x,EF=2y,
过D作DH⊥EF于H,则EH=FH=y,∠EDH=∠FDH=α,
由勾股定理得:DH=
| x2-y2 |
sinα=
| EH |
| DE |
| y |
| x |
| DH |
| DE |
| DH |
| x |
所以sinαcosα=
| y•DH |
| x2 |
∵由三角形面积公式得:
| 1 |
| 2 |
| 1 |
| 2 |
∴EQ=
| EF×DH |
| DF |
| 2yDH |
| x |
∴sin2a=
| EQ |
| DE |
| 2yDH |
| x2 |
∴sin2α=2sinαcosα,

如图3,过C作CW⊥AB于W,
则CW=AC×sin2α=bsin2α,
∴S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
∵sin2α=2sinαcosα,
∴S△ABC=absinαcosα.

如图4,过D作DT⊥AB于T,DZ⊥AC于Z,
∵AD是角平分线,
∴DT=DZ,
设DT=DZ=e,
根据三角形的面积公式得:S△ABC=S△ADB+S△ADC,
absinαcosα=
| 1 |
| 2 |
| 1 |
| 2 |
∴DT=e=
| 2absinαcosα |
| a+b |
在Rt△ATD中,AD=
| DT |
| sinα |
| ||
| sinα |
| 2abcosα |
| a+b |
点评:本题考查了解直角三角形,三角形的面积公式,平行线分线段成比例定理,勾股定理的应用,题目比较好,综合性比较强,难度偏大.

练习册系列答案
相关题目
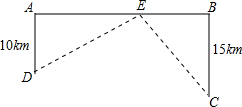 如图,河岸上A、B两点相距25km,C、D为两村庄,DA⊥AB于点A,CB⊥AB与点B,已知DA=10km,CB=15km,现在AB上建一个水泵站E,使得C,D两村到E站的距离相等.求E应建在距A多远处?
如图,河岸上A、B两点相距25km,C、D为两村庄,DA⊥AB于点A,CB⊥AB与点B,已知DA=10km,CB=15km,现在AB上建一个水泵站E,使得C,D两村到E站的距离相等.求E应建在距A多远处?