题目内容
若方程x2-kx+6=0的两根分别比方程x2+kx+6=0的两根大5，则k的值是 ．
考点：根与系数的关系
专题：计算题
分析：设方程x2+kx+6=0的两根分别为a、b，则方程x2-kx+6=0的两根分别为a+5，b+5，根据根与系数的关系得到a+b=-k，a+5+b+5=k，然后消去a+b即可得到k的方程，然后解关于k的方程即可．
解答：解：设方程x2+kx+6=0的两根分别为a、b，则方程x2-kx+6=0的两根分别为a+5，b+5，
根据题意得a+b=-k，a+5+b+5=k，
所以10-k=k，
解得k=5．
故答案为：5．
根据题意得a+b=-k，a+5+b+5=k，
所以10-k=k，
解得k=5．
故答案为：5．
点评：本题考查了根与系数的关系：若x1，x2是一元二次方程ax2+bx+c=0（a≠0）的两根时，x1+x2=-
，x1x2=
．
| b |
| a |
| c |
| a |
练习册系列答案
挑战100单元检测试卷系列答案
相关题目
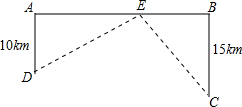如图，河岸上A、B两点相距25km，C、D为两村庄，DA⊥AB于点A，CB⊥AB与点B，已知DA=10km，CB=15km，现在AB上建一个水泵站E，使得C，D两村到E站的距离相等．求E应建在距A多远处？
如图，在△ABC中，∠A=30°，∠B=45°，AC=10cm，求AB的长．已知点（-4，y1），（2，y2），（-1，y3）都在直线y=-
x+c（c为常数）上，则y1、y2、y3的大小关系为（ ）
| 1 |
| 2 |
| A、y1＜y2＜y3 |
| B、y2＜y3＜y1 |
| C、y3＜y1＜y2 |
| D、y2＜y1＜y3 |