题目内容
已知在△ABC中，∠A=40°，高BE、CF相交于点O，求∠BOC的度数．考点：三角形内角和定理
专题：
分析：根据直角三角形两锐角互余求出∠ABE的度数，再根据三角形的一个外角等于和它不相邻的两个内角的和即可求出∠BOC的度数．
解答：解：∵BE，CF是高，
∴∠AEB=∠BFC=90°，
又∵∠A=40°，
∴∠ABE=90°-40°=50°，
∴∠BOC=∠BFC+∠ABE=140°．
∴∠AEB=∠BFC=90°，
又∵∠A=40°，
∴∠ABE=90°-40°=50°，
∴∠BOC=∠BFC+∠ABE=140°．
点评：本题考查了直角三角形两锐角互余的性质和三角形的外角性质，熟练掌握性质是解题的关键．
练习册系列答案
步步高达标卷系列答案
相关题目
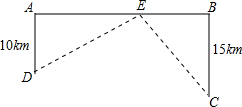如图，河岸上A、B两点相距25km，C、D为两村庄，DA⊥AB于点A，CB⊥AB与点B，已知DA=10km，CB=15km，现在AB上建一个水泵站E，使得C，D两村到E站的距离相等．求E应建在距A多远处？已知点（-4，y1），（2，y2），（-1，y3）都在直线y=-
x+c（c为常数）上，则y1、y2、y3的大小关系为（ ）
| 1 |
| 2 |
| A、y1＜y2＜y3 |
| B、y2＜y3＜y1 |
| C、y3＜y1＜y2 |
| D、y2＜y1＜y3 |
点A，B在数轴上分别表示有理数a，b，A，B两点之间的距离表示为AB，回答下列问题：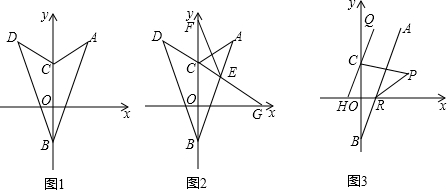
已知一次函数y=kx+b的图象如图所示，则关于x的不等式kx+b＞0的解集是（ ）| A、x＞-2 | B、x＜2 |
| C、x＞2 | D、x＜-2 |
已知：如图，锐角△ABC的两条高BD、CE相交于点O，且OB=OC．试说明△ABC是等腰三角形．