题目内容
4．解方程：$\frac{1}{x（x+1）}$+$\frac{1}{（x+1）（x+2）}$+$\frac{1}{（x+2）（x+3）}$=$\frac{1}{x+3}$．分析 根据解分式方程的方法，将分式方程转换为整式方程，再根据解整式方程的步骤，解方程，最后检验．
解答 解：两边同时乘以x（x+1）（x+2）（x+3），
得：（x+2）（x+3）+x（x+3）+x（x+1）=x（x+1）（x+2），
整理，得：-（x+1）（x-6）（x+1）=0，
解得：x=6或x=-1，
检验：当x=6时，最简公分母x（x+1）（x+2）（x+3）≠0，
当x=-1时，最简公分母x（x+1）（x+2）（x+3）=0，
∴x=6是原分式方程的解．
点评 本题主要考查解分式方程．将分式方程转化为整式方程是解决此题的关键，此外，要注意检验．
练习册系列答案
导学教程高中新课标系列答案
相关题目
如图，AC=7，BC=3，点M是AB的中点，求AM，CM的长度．
9．
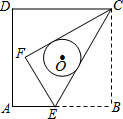如图，正方形ABCD的边长为9，点E是AB上的一点，将△BCE沿CE折叠至△FCE，若CF，CE恰好与以正方形ABCD的中心为圆心的⊙O相切，则折痕CE的长为（ ）
如图，正方形ABCD的边长为9，点E是AB上的一点，将△BCE沿CE折叠至△FCE，若CF，CE恰好与以正方形ABCD的中心为圆心的⊙O相切，则折痕CE的长为（ ）| A． | 4$\sqrt{3}$ | B． | $\frac{8}{3}$$\sqrt{3}$ | C． | 4$\sqrt{5}$ | D． | 6$\sqrt{3}$ |