题目内容
20.已知一元二次方程x2+bx+c=0的一根为x1=1,另一根为1<x2<2,给出下列结论:①1<c<2;②-3<b<-2;③b+c=-1.其中正确结论的个数是( )| A. | 3 | B. | 2 | C. | 1 | D. | 0 |
分析 由根的意义得出1+b+c=0,得出b+c=-1,③正确;设y=x2+bx+c,由另一根为1<x<2,得出图象可知当x=2时,y>0,得出4+2b+c>0,得出b>-3,由对称轴得出b<-2,得出-3<b<-2,②正确;由③和②得出-3<-1-c<-2,因此1<c<2,①正确;即可得出结果.
解答 解:∵一元二次方程x2+bx+c=0的一根为x=1,
∴1+b+c=0,
∴b+c=-1,
∴③正确;
设y=x2+bx+c,
∵另一根为1<x<2,
∴图象如图所示: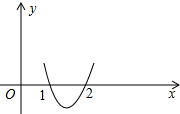
∴当x=2时,y>0,
即:4+2b+c>0,
∵b+c=-1,
∴b>-3,
∵对称轴x=-$\frac{b}{2}$>1,
∴b<-2,
∴-3<b<-2,
∴②正确;
∵b+c=-1,-3<b<-2,
∴-3<-1-c<-2,
解得:1<c<2,
∴①正确;
故选A.
点评 本题主要考查了抛物线与x轴的交点,在解题时要能够灵活应用抛物线与一元二次方程的关系是本题关键,注意数形结合.

练习册系列答案
相关题目
5.设a=-(-3-2)2,b=(-3)×(-2),c=(-3)2÷(-2)2,则( )
| A. | b>a>c | B. | b>c>a | C. | a>b>c | D. | c>a>b |
10.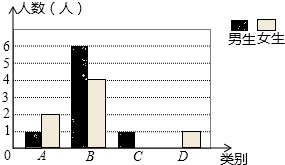 某校七年级共有200名学生,在一次数学测验后,为了解本次测验的成绩情况,从中随机抽取了部分学生的成绩进行统计,并制作了如图表:
某校七年级共有200名学生,在一次数学测验后,为了解本次测验的成绩情况,从中随机抽取了部分学生的成绩进行统计,并制作了如图表:
请你根据以上信息,解答下列问题:
(1)写出a,b,d的值并补全条形图;
(2)请你估计该校七年级共有多少名学生本次成绩不低于80分.
 某校七年级共有200名学生,在一次数学测验后,为了解本次测验的成绩情况,从中随机抽取了部分学生的成绩进行统计,并制作了如图表:
某校七年级共有200名学生,在一次数学测验后,为了解本次测验的成绩情况,从中随机抽取了部分学生的成绩进行统计,并制作了如图表:| 等级 | 分数 | 频数 | 频率 |
| A | 90≤x≤100 | 3 | 0.15 |
| B | 80≤x<90 | 10 | a |
| C | 70≤x<80 | b | 0.2 |
| D | 60≤x<70 | c | d |
| 合计 | 1 |
(1)写出a,b,d的值并补全条形图;
(2)请你估计该校七年级共有多少名学生本次成绩不低于80分.
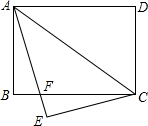 如图,矩形ABCD中,AB=6,BC=8,将△ACD沿对角线AC翻折得△ACE,AE交BC于点F,将△CEF绕点C逆时针旋转α角(0°<α<180°)得△CE′F′,点E、F的对应点分别为E、F的对应点分别为E′、F′.旋转过程中直线CF′、E′F′分别交直线AE于点M、N,当△F′NM是等腰三角形且MN=MF′时,则MN=$\frac{275}{56}$.
如图,矩形ABCD中,AB=6,BC=8,将△ACD沿对角线AC翻折得△ACE,AE交BC于点F,将△CEF绕点C逆时针旋转α角(0°<α<180°)得△CE′F′,点E、F的对应点分别为E、F的对应点分别为E′、F′.旋转过程中直线CF′、E′F′分别交直线AE于点M、N,当△F′NM是等腰三角形且MN=MF′时,则MN=$\frac{275}{56}$.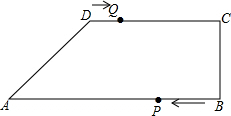 四边形ABCD中,AB∥CD,CB⊥CD,AB=18cm,BC=6cm,CD=10cm,点P在线段BA上从B向A运动,速度为2cm/s,点Q在线段DC上从D向C运动,速度为1cm/s,P,Q两点同时开始运动.设运动时间为T秒.
四边形ABCD中,AB∥CD,CB⊥CD,AB=18cm,BC=6cm,CD=10cm,点P在线段BA上从B向A运动,速度为2cm/s,点Q在线段DC上从D向C运动,速度为1cm/s,P,Q两点同时开始运动.设运动时间为T秒.