题目内容
8.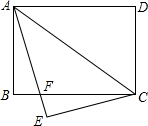 如图,矩形ABCD中,AB=6,BC=8,将△ACD沿对角线AC翻折得△ACE,AE交BC于点F,将△CEF绕点C逆时针旋转α角(0°<α<180°)得△CE′F′,点E、F的对应点分别为E、F的对应点分别为E′、F′.旋转过程中直线CF′、E′F′分别交直线AE于点M、N,当△F′NM是等腰三角形且MN=MF′时,则MN=$\frac{275}{56}$.
如图,矩形ABCD中,AB=6,BC=8,将△ACD沿对角线AC翻折得△ACE,AE交BC于点F,将△CEF绕点C逆时针旋转α角(0°<α<180°)得△CE′F′,点E、F的对应点分别为E、F的对应点分别为E′、F′.旋转过程中直线CF′、E′F′分别交直线AE于点M、N,当△F′NM是等腰三角形且MN=MF′时,则MN=$\frac{275}{56}$.
分析 根据等腰三角形的性质得到∠MNF′=∠CF′E′,由折叠的性质得到∠NF′M=∠CF′E′,∠CF′E′=∠CFE,等量代换得到∠MNF=∠CFE,求得F′E′∥BC,根据平行线的性质得到∠FCF′=∠DCB=90°,过M作MH⊥CD,交DC的延长线于H,MI⊥BC,推出△CF′E′∽△CNH,CI=FI,由折叠的性质得:AF=CF,设EF=x,在Rt△CEF中由勾股定理得x2+36=(8-x)2,求得BF=EF=$\frac{7}{4}$.CF=$\frac{25}{4}$,于是得到CF:EF:CE=25:7:24,由于△CF′E′∽△CNH,由相似三角形的性质得到NH:HC:CM=7:24:25,求出MH=$\frac{1}{2}$CF=$\frac{25}{8}$,得到MC=$\frac{25}{8}$×$\frac{25}{7}$=$\frac{625}{56}$,即可得到结论.
解答 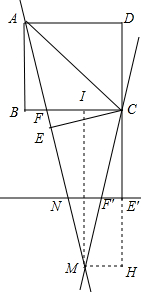 解:∵MN=MF′,
解:∵MN=MF′,
∴∠MNF′=∠MF′N,
∵∠NF′M=∠CF′E′,∠CF′E′=∠CFE,
∴∠MNF′=∠CFE,
∴F′E′∥BC,
∴∠F′E′C=∠DCB=90°,
过M作MH⊥CD,交DC的延长线于H,MI⊥BC,
∴△CF′E′∽△CMH,CI=FI,
由折叠的性质得:AF=CF,
设EF=x,
在Rt△CEF中,
由勾股定理得x2+36=(8-x)2,
解得:x=$\frac{7}{4}$,
∴BF=EF=$\frac{7}{4}$.CF=$\frac{25}{4}$,
∴CF:EF:CE=25:7:24,
∵△CF′E′∽△CMH,
∴MH:HC:CM=7:24:25,
∴MH=$\frac{1}{2}$CF=$\frac{25}{8}$,
∴MC=$\frac{25}{8}$×$\frac{25}{7}$=$\frac{625}{56}$,
∴MF′=CM-CF=$\frac{625}{56}$-$\frac{25}{4}$=$\frac{275}{56}$.
故答案为:$\frac{275}{56}$.
点评 本题考查了旋转的性质,折叠的性质,矩形的性质相似三角形的判定和性质,勾股定理,熟练掌握各性质定理是解题的关键.

 备战中考寒假系列答案
备战中考寒假系列答案 如图,已知在△ABC中,∠C=90°,AB的垂直平分线交BC于D,垂足为E,∠CAD:∠DAB=2:1,求∠BAC的度数.
如图,已知在△ABC中,∠C=90°,AB的垂直平分线交BC于D,垂足为E,∠CAD:∠DAB=2:1,求∠BAC的度数.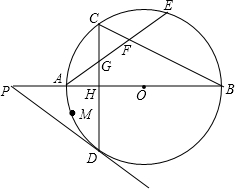 如图,AB是⊙O的直径,弦CD⊥AB于H,点E在$\widehat{BC}$上,且$\widehat{CE}=\widehat{AD}$,AE与CD交于点G,与BC交于点F.
如图,AB是⊙O的直径,弦CD⊥AB于H,点E在$\widehat{BC}$上,且$\widehat{CE}=\widehat{AD}$,AE与CD交于点G,与BC交于点F. 如图,已知AD为△ABC的高线,AD=BC,以AB为底边作等腰Rt△ABE,连接ED,EC,延长CE交AD于F点,下列结论:①△ADE≌△BCE;②CE⊥DE;③BD=AF;④S△BDE=S△ACE,其中正确的有( )
如图,已知AD为△ABC的高线,AD=BC,以AB为底边作等腰Rt△ABE,连接ED,EC,延长CE交AD于F点,下列结论:①△ADE≌△BCE;②CE⊥DE;③BD=AF;④S△BDE=S△ACE,其中正确的有( )