题目内容
15.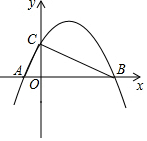 如图,在平面直角坐标系中,抛物线y=ax2+bx+4与坐标轴分别交于点A、点B、点C,并且∠ACB=90°,AB=10.
如图,在平面直角坐标系中,抛物线y=ax2+bx+4与坐标轴分别交于点A、点B、点C,并且∠ACB=90°,AB=10.(1)求证:△OAC∽△OCB;
(2)求该抛物线的解析式;
(3)若点P是(2)中抛物线对称轴上的一个动点,是否存在点P使得△PAC为等腰三角形?若存在,请直接写出点P的坐标;若不存在,请说明理由.
分析 (1)根据余角的性质得到∠CAO=∠BCO,根据相似三角形的判定定理即可得到结论;
(2)根据相似三角形的性质得到$\frac{OC}{OB}=\frac{OA}{OC}$,得到A(-2,0),B(8,0),解方程组即可得到结论;
(3)设P(3,n),根据两点间的距离得到AC=2$\sqrt{5}$,AP=$\sqrt{(-2-3)^{2}+{n}^{2}}$=$\sqrt{25+{n}^{2}}$,PC=$\sqrt{{3}^{2}+(n-4)^{2}}$,①当AC=AP时,②当AC=CP时,③当AP=CP时,解方程即可得到结论.
解答 解:(1)∵∠ACB=∠AOC=∠BOC=90°,
∴∠CAO+∠ACO=∠ACO+∠BCO=90°,
∴∠CAO=∠BCO,
∴△OAC∽△OCB;
(2)∵在y=ax2+bx+4中,当x=0,y=4,
∴OC=4,
∵△OAC∽△OCB,
∴$\frac{OC}{OB}=\frac{OA}{OC}$,
∴$\frac{4}{OB}$=$\frac{10-OB}{4}$,
∴OB=2或OB=8,
∴A(-2,0),B(8,0),
∴$\left\{\begin{array}{l}{4a-2b+4=0}\\{64a+8b+4=0}\end{array}\right.$,
∴$\left\{\begin{array}{l}{a=-\frac{1}{4}}\\{b=\frac{3}{2}}\end{array}\right.$,
∴该抛物线的解析式为y=-$\frac{1}{4}$x2+$\frac{3}{2}$x+4;
(3)存在,∵y=-$\frac{1}{4}$x2+$\frac{3}{2}$x+4=-$\frac{1}{4}$(x-3)2+$\frac{13}{4}$,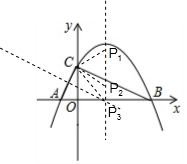
∴抛物线的对称轴为:直线x=3,
∴设P(3,n),
∵A(-2,0),C(0,4),
∴AC=2$\sqrt{5}$,AP=$\sqrt{(-2-3)^{2}+{n}^{2}}$=$\sqrt{25+{n}^{2}}$,PC=$\sqrt{{3}^{2}+(n-4)^{2}}$,
∵△PAC为等腰三角形,
①当AC=AP时,即$\sqrt{25+{n}^{2}}$=2$\sqrt{5}$,
此方程无实数根,这种情况不存在;
②当AC=CP时,即2$\sqrt{5}$=$\sqrt{{3}^{2}+(n-4)^{2}}$,
解得:n=4+$\sqrt{11}$,n=4-$\sqrt{11}$,
③当AP=CP时,即$\sqrt{25+{n}^{2}}$=$\sqrt{{3}^{2}+(n-4)^{2}}$,
解得:n=0,
∴P(3,4+$\sqrt{11}$),(3,4-$\sqrt{11}$),(3,0).
点评 本题考查了相似三角形的判定,待定系数法确定函数关系式,等腰三角形的判定,正确的理解题意是解题的关键.

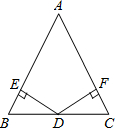 如图,在△ABC中,∠B=∠C,D为BC中点,若由点D分别向AB、AC作垂线段DE、DF,则能说明△BDE≌△CDF的理由是( )
如图,在△ABC中,∠B=∠C,D为BC中点,若由点D分别向AB、AC作垂线段DE、DF,则能说明△BDE≌△CDF的理由是( )| A. | AAS | B. | SAS | C. | HL | D. | SSS |
| A. | 0≤d<5 | B. | 0<d<5 | C. | d=5 | D. | d>5 |
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
| A. | 30.01mm | B. | 30.05mm | C. | 29.08mm | D. | 29.97mm |
| A. | 该二次函数图象开口向上 | B. | 点A的坐标随m的变化而变化 | ||
| C. | 点A、B间的距离为6 | D. | 当m<2时,b>0 |
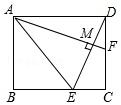 如图所示,在矩形ABCD中,F是DC上一点,AE平分∠BAF交BC于点E,且DE⊥AF,垂足为点M,BE=3,AE=2$\sqrt{6}$,则MF的长是$\frac{\sqrt{15}}{15}$.
如图所示,在矩形ABCD中,F是DC上一点,AE平分∠BAF交BC于点E,且DE⊥AF,垂足为点M,BE=3,AE=2$\sqrt{6}$,则MF的长是$\frac{\sqrt{15}}{15}$.